Cet article est une reproduction du dossier que j’ai écrit pour Podcastscience et je vous engage à vous abonner à ce podcast. Pour les plus flemmards, le texte et l’audio dans la suite…
[audio:http://www.podcastscience.fm/podpress_trac/web/1817/0/104-Zero_optimise.mp3]
Dans ce dossier, nous allons raconter la longue histoire de la découverte d’un nombre. Un simple nombre qui pourtant a tout changé et permet aujourd’hui l’existence des plus grandes théories (mais ça, nous le verrons la semaine prochaine). Eh oui, après vous avoir parlé de l’infini, de pi, aujourd’hui on s’attaque au zéro!
La vie sans rien
Mais avant de parler du zéro lui même, nous allons un peu parler du temps où l’on vivait sans cet étrange nombre. On a peu de traces avant l’apparition de l’écriture, pour autant, on peut avoir des indices sur l’existence sans le nul en observant notre vie contemporaine. On se rend alors vite compte que l’on n’a pas vraiment besoin de lui dans notre vie de tous les jours : personne n’a besoin d’aller acheter zéro baguettes, d’inviter zéro amis à une soirée ou de passer zéro secondes sur un travail (surtout ce dernier point, qui est un sous-entendu universel de l’humanité procrastinatrice). Ou plus précisément, on peut en avoir le besoin mais alors on a pas besoin de l’exprimer : je ne vais pas lister tous les produits dont j’ai besoin sur une liste en mettant un zéro dessus!
En fait, à l’aube des temps humains, les gens faisaient apparement seulement la distinction entre un et beaucoup. On était capable de dire s’il y avait un arbre. Et s’il y en avait plus, il y en avait tout de suite beaucoup. Remarquons que cela aussi est peu différent aujourd’hui, du moins sans compter, tant qu’il y a 4–5 objets, on est capable de tout de suite dire leur nombre et ensuite il y en a “beaucoup” (faites le test chez vous, ça marche!).
Les hommes réussissaient quand même à différentier les groupes, en utilisant la bijection! Comme on l’a vu dans le dossier sur l’infini, en plaçant sur le sol un caillou à chaque objet que l’on voit, on peut savoir qu’il y a plus d’éléments dans un groupe qu’un autre sans compter. Mais pour y arriver sans bijection et de manière absolue, il faut savoir compter… Et donc les hommes se sont mis à compter justement. Et comme il ne savaient pas forcément encore écrire, ils utilisaient ce qu’ils avaient de plus facilement disponible : les parties de leur corps! L’évolution, la selection génétique et beaucoup de hasard nous ont amenés à avoir 5 doigts sur chaque main et pied. On pouvait alors facilement compter jusqu’à 5 et quand il fallait plus, on donne un nom au 5 et on pouvait recommencer à 1, histoire de pouvoir continuer à compter avec les parties de son corps :
1,2,3,4,5,5 et 1,5 et 2, 5 et 3, etc.
Et il suffisait d’avoir un nouveau mot pour 10, 15, 20, 25, etc. pour pouvoir compter autant qu’on voulait.
C’est ce qu’on appelle compter en base 5! Et hasard de l’anatomie, 5 est justement la base préférée des hommes quelle que soit la culture. Il y avait d’autres bases aussi, le plus souvent liées à une partie de notre corps : 5, 10 (deux mains), 20 (mains et pieds) et… 60 qu’utilisaient les Babyloniens!
 |
 |
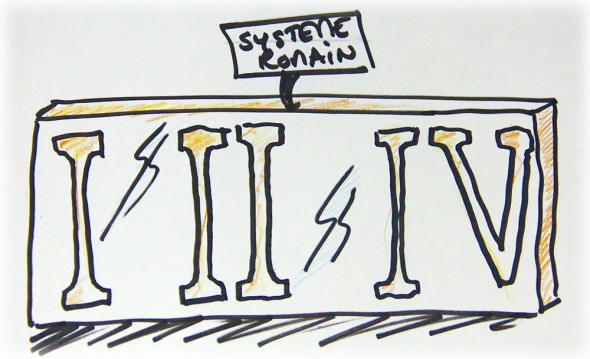
Remarquez que ces systèmes de numérotations ressemblent beaucoup au système romain (même s’il est postérieur), que l’on connait tous.
Avec ces systèmes, les gens pouvaient compter. Pour autant, ces systèmes n’avaient pas de zéro; ce concept n’existait tout simplement pas! Pour dire qu’on a zéro baguette, il suffit de dire “nous n’avons pas de baguettes”, aucun besoin de créer un nombre pour exprimer le manque de quelque chose! Les gens vécurent longtemps sans zéro car ils n’en avaient pas besoin. Et dans les esprits de cette époque, il aurait été bien saugrenu de créer un symbole pour représenter ce rien.
Un rien facilite le comptage
Les Grecs, les Egyptiens et la plupart des peuples anciens avaient des systèmes plus ou moins sophistiqués mais tous basés sur cette même idée. Le peuple qui a vraiment révolutionné la numérotation (tout comme il révolutionna bien d’autres choses) sont les Babyloniens.
Les Babyloniens représentaient les chiffres comme s’ils dessinaient symboliquement un abaque. Chaque groupe de symboles représentait le nombre de pierre qu’on avait déplacé sur l’abaque. La véritable nouveauté de ce système est que, comme le nôtre, il fonctionnait par colonnes. L’unité babylonienne ressemble à un Y ou à un clou. Quand un Babylonien écrivait YYY, le premier symbole représentait les “centaines”, le second les “dizaines” et le troisième les “unités”. Si je met ici des guillemets c’est que les Babyloniens ne comptaient pas comme nous, mais en base 60. Ainsi, le premier Y représentait en fait 3600, le second 60 et le troisième 1. Comme nous écrivons 123 pour dire en fait 1×100+2×10+3, les Babyloniens écrivaient YYY pour dire 1×3600+1×60+1.
Reste qu’aussi ingénieux soit-il, ce système présentait un problème de taille. Le nombre YY pouvait aussi bien vouloir dire 3601 que 3660 ou encore 61. En effet, si l’un des chiffres de la décomposition dans la base ne présentait pas d’éléments, les Babyloniens se contentaient de laisser un espace. Il était alors très difficile de différencier les chiffres avec précision. A la recherche d’une solution pour palier ce problème, les Babyloniens ont inventé le zéro! A cette époque, il n’est pas encore un nombre, il se contente seulement d’être la représentation d’un espace, un rien mais qui permet déjà de lever toute ambiguité sur le système de numérotation. C’est autour de 300 avjc que les Babyloniens ont commencé à utilisé cet espèce de Y penché pour le zéro.
Reste que ce zéro là n’était pas un nombre, c’était juste un espace dans le système de numérotation, une ponctuation des mathématiques, en somme. Les Babyloniens auraient par exemple été bien incapable de le classer parmi les autres nombres et l’auraient peut être amené à la droite du 9 comme sur nos claviers, les malheureux! Les Babyloniens n’étaient pas les seuls à utiliser un système de numérotation où les chiffres étaient sur des colones, les Mayas aussi. Et eux choisirent justement de commencer à compter à partir de zéro. Reste qu’à cette époque, zéro n’est pas encore réellement un nombre ou du moins on n’a pas retrouvé d’utilisation mathématique.
Le vertige des Grecs
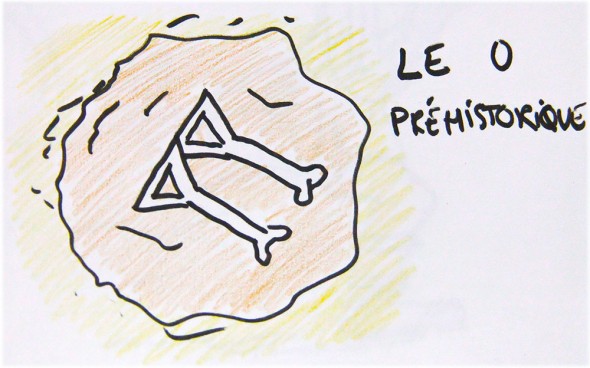
Les grecs détestaient le zéro. Ils avaient pourtant connaissance du système babylonien qu’ils utilisaient entre autres pour leur calculs astronomiques mais se dépêchaient de le reconvertir dans leur système pur, sans ce nombre vide. Il est à noter que les grecs écrivaient le zéro “o” pour omikron, dont la ressemblance avec notre zéro actuel est un pur hasard, on va rapidement voir pourquoi.
Une des premières raisons de cette détestation de ce simple nombre est que selon les croyance grecques, avant la création, il y avait le vide et le chaos ; zéro leur était alors inexorablement associé.
Mais ce n’était pas la seule raison de ce rejet, loin de là! Le zéro était en contradiction ou pire, paradoxal, pour la plupart des croyances grecques. Par exemple zéro additionné à lui même reste le même nombre nul. Ce qui contredit directement le principe d’Archimède qui dit qu’en ajoutant n’importe quel nombre à lui-même suffisament de fois, on dépasse tout nombre. De plus, les grecs avaient une vision géométrique des nombres; n’importe quel nombre était associé à un segment, une multiplication revenait alors à dilater le segment et une division à le contracter. Mais à quoi correspondrait une multiplication par zéro? Et à quel type de segment correspondrait ce nombre étrange? Comme n’importe quel nombre multiplié par zéro donne justement zéro, le segment est cassé de manière irréversible, zéro est une brute qui casse tout ce qu’il touche, les grecs n’en veulent pas!
De nous jours, la définition de zéro est justement qu’additionné à n’importe quel nombre, il laisse le nombre inchangé. En revanche, le fait que sa multiplication par n’importe quel nombre donne zéro se démontre! L’ensemble des nombres entiers relatifs (qui n’existe pas encore certes, mais c’est ici une apparté!) ou plus simplement nommé ensemble de tous les nombres entiers positifs est ce que l’on appelle en mathématiques un groupe pour l’addition. C’est à dire qu’il respecte les 4 règles suivantes :
- Si l’on prend deux nombres quelconques de ce groupe, leur somme appartient aussi au groupe. Par exemple 2 et 5 sont des entiers relatifs et leur somme 7 aussi.
- L’addition respecte l’associativité. C’est à dire qu’on peut changer la place des parenthèses : 2+(3+4)=(2+3)+4
- Le groupe possède un élément neutre, c’est à dire un élément ‘e’ tel que pour n’importe quel nombre ‘a’, a+e=e+a=a. C’est justement cet élément neutre que l’on appelle zéro pour l’addition.
- Chaque élément possède un inverse. C’est à dire que pour chaque nombre ‘a’, il existe un nombre ‘b’ tel que a+b=e, l’élément neutre. Par exemple, pour 5, il existe -5 tel que 5+(-5)=0!
Prenons par exemple 4 (ça marche bien sur avec tous les nombres), En utilisant la factorisation et la propriété du neutre pour l’addition, on peut écrire :
0x4+0x4=4x(0+0)=4×0
En simplifiant par 4×0, on obtient 4×0=0. Le zéro transforme par la multiplication n’importe quel nombre en lui-même!
[Dessin – Les mathématiciens savent démontrer que 0x0=0)
Revenons à nos grecs anciens. Le zéro transformait donc le nombre-segment grec en un point, on détruisait le segment, ce qui était impensable dans la pensée grecque et surtout enlevait toute possibilité d’inversion du phénomène… Mais justement, que se passait-il si on divisait par zéro?
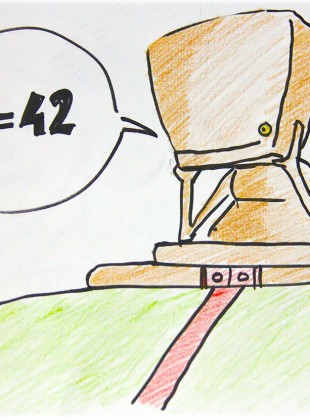
Tout le monde le sait depuis la petite école, comme il est interdit de prononcer le nom de “vous savez qui”, il est INTERDIT DE DIVISER PAR ZERO. C’est un phénomène assez amusant et aussi l’objet d’un mème! En fait il n’est pas exactement interdit de diviser par zéro, c’est juste que si vous vous l’autorisez ne serait-ce qu’une seule fois, vous pouvez démontrer tout et n’importe quoi. Par exemple, nous allons démontrer avec une division par zéro un bien joli résultat.
On sant que pi x 0 = 42 x 0 car tout nombre multiplié à zéro fait zéro. Une division par zéro plus tard on a alors
pi=42.
Jusque ici rien de très étonnant, on savait depuis longtemps que 42 était la réponse à tout ce qui existe mais comme on a pu le voir dans le dossier sur le théorème de Gödel ou celui sur l’infini, s’autoriser une contradiction (bah oui parce que pi n’est pas égal à 42) amène à une théorie contradictoire où tout résultat et son contraire est vrai. Alors certes on peut s’amuser à diviser par zéro mais alors, plus rien n’a de sens!
Le rejet du zéro par les grecs était avant tout philosophique, il représentait une réelle plaie pour la pensée de l’époque, un peu comme le furent les irrationnels. Remarquons que l’infini avait déjà pas mal agacé les grecs entre autrse avec le paradoxe de Zénon. En fait, zéro et infini sont intimement liés, comme nous le verrons plus en détail la semaine prochaine.
Mais celui qui a de loin le plus empêché le zéro d’arriver pleinement chez les Grecs à cette époque-là et plus tard en Europe est Aristote. En effet, sa pensée a influencé l’Europe pendant les siècles suivants et il était le plus fervent opposant au nombre étrange. Cette opposition d’Aristote a laissé aujourd’hui quelques restes comme l’expression “la nature a horreur du vide”.
Des particules élémentaires oui mais sûrement pas du vide
A l’époque, la théorie des atomes commençait à naître. Or les atomes impliquent d’avoir du vide, en effet, entre ces atomes il y a beaucoup de vide… et dans l’univers, la théorie atomiste imposait un vide infini. Pour exemple, si l’on retire le vide de tous les atomes de l’empire state building, on obtient quelque chose pas plus grand que la taille d’un grain de riz.
Aristote refusait de croire au vide, il acceptait l’idée de particules élémentaires mais rejettait la notion d’atomes et considérait que toute la matière était constituée des 4 éléments : Eau, Feu, Air et Terre. Et il considérait la matière comme continue, ne s’interrompant jamais. Il est assez ironique de remarquer que les théories modernes de cosmologie reviennent sur cette notion de vide absolu en donnant non seulement une courbure à ce vide (avec la relativité générale) ou encore en postulant que le champ de Higgs est partout et interagit sur les particules.
Reste que pour palier ce problème avec le vide et surtout avec l’infini, les philosophes de l’époque complétèrent la théorie atomiste d’une manière particulièrement poétique. Ils postulèrent que l’univers était en fait dans une gigantesque sphère, où, bien sûr, la Terre était au centre. Cette sphère englobante était un globe bleu, incrusté de petits points brillants : les étoiles. L’univers devenait fini et Aristote déclarait que les mathématiciens n’avaient pas besoin d’infini, ni de l’utiliser. Or pour rejeter l’infini, il faut rejeter le vide, les deux sont intimement liés. En effet, a partir du moment où l’on accepte l’existence du vide, comme zéro ajouté à lui même reste zéro, il y a aussi une infinité de vide!
Pour l’anecdote, Archimède calcula qu’il fallait 1051 grains de sable pour remplir la sphère de l’univers. Ce nombre était tellement grand que le système de numérotation grec ne pouvait pas l’écrire!
Ce système a perduré pendant de nombreux sciècles pour une raison très simple: il prouvait de manière irréfutable l’existence de Dieu. La grosse sphère incrustée de points lumineux qui englobait l’univers tournait et il fallait bien une force extérieure pour la faire tourner, cela ne pouvait être que Dieu!
1400 ans sans entendre parler de rien et le bug de l’an 2000
Une fois qu’Aristote eut fait son oeuvre, impossible pour le zéro d’entrer en Grèce. Et avec l’invasion des Romains, le neutre fut rayé d’Europe pendant plus de 1400 ans… Les 7 sciècles d’ère romaine n’ont pas spécialement marqué l’histoire mathématique, l’auteur de “Zero, Biography of a Dangerous Idea”, qui a servi de base à ce dossier résume cela en disant que le meurtre d’Archimède fut sans doute la contribution la plus notable des Romains à cette science!
Pour s’en convaincre plus encore, il suffit de regarder leur système de numérotation que l’on utilise tous encore parfois; il est bien loin de l’innovation Babylonienne. Pendant les 7 sciècles qui suivirent les romains, le zéro ne montra pas non plus son nez, ce qui laissa tout le temps aux moines de faire n’importe quoi…
Les moines à cette époque n’avaient besoin des maths que pour deux activités : la prière et l’argent. Pour organiser les prières, il était nécessaire de créer un calendrier et c’est exactement ce à quoi s’attela Dyonysius Exiguus sur les ordres du pape Jean 1er. En traduisant des tables provenant de l’Est du continent, il découvrit qu’il pourrait calculer la date de naissance de Jésus Christ. En faisant rapidement quelques calculs, il décida que l’année courante était la 525e année depuis la naissance du Christ (soit dit en passant, il s’était en fait trompé de 4 ans…).Et en toute logique, il choisit l’année 1 pour la naissance du Christ. Remarquez que l’on refuse aussi de dire qu’un bébé a zéro ans. Pendant sa première année, on commence à compter en jours, puis en semaines, puis en mois, puis enfin en années en banissant la phrase toute simple “il est beau hein, il a zéro ans”. Il est quand même balo que pour mettre le Christ au centre de leur calendrier, les moines ont tout simplement oublié son année de naissance.
Le zéro ayant été bani par Aristote, les années s’organisaient donc sans lui
… –2 –1 1 2 …
Cette simple décision nous fait encore aujourd’hui faire des erreurs. Par exemple, 6 milliards de personnes (ce n’esst pas rien) ont fêté le nouveau millénaire un an trop tôt, sans année zéro, celui-ci commence en 2001!
[Dessin d’un mec tout seul dans son lit pendant que les mec font la fete à la fenetre “Les cons!”]
Mais pire encore, comme on l’a vu au-dessus, sans zéro, pas de neutre et donc pas de groupe au sens mathématique; on n’a plus le droit aux soustraction sans erreurs… Grâce à ce zéro, on peut inverser l’opération d’addition et simplifier les équations, c’est ce qui nous permet d’écrire que
x+5=3
est équivalent à
x=5–3=2
Sans ce neutre, on ne peut plus faire tout ça! Reprenez la ligne des nombres sans zéro de tout à l’heure :
… –5 –4 –3 –2 –1 1 2 3 4 5 …
5, à qui l’on soustrait cinq unités donne –1 : 5–5=1. Mais pire encore, 5+(–5)=1. L’addition n’est même plus commutative! Sans cette simple année zéro, on ne peut pas soustraire des dates, et on ne peut pas additionner indifféremment des dates positives avec des dates négatives ou des dates négatives avec des dates positives! C’est exactement ce type d’erreur que fit le Washington Post en annonçant fièrement que comme le Christ était né en –4, le nouveau millénaire devait être fêté en 1996!
A titre de remarque, cette notion de neutre est indispensable pour pouvoir inverser une opération. Dans le cas de la multiplication, c’est le 1 qui joue ce rôle de neutre.
Quant au fait de compter les années à partir de la naissance de Jesus Christ plutot qu’un autre, sachez que les astronomes utilisent une autre référence, elle aussi complètement arbitraire, mais pas biblique, en particulier pour y ajouter le zéro et faciliter les calculs.
Mais si nous avons autant fêté l’année 2000, c’est avant tout parce que l’on aime les nombre avec pleins de zéros! Malgré la lutte d’Aristote pour le faire disparaître, qui n’a jamais joué avec le compteur d’une pompe à essence pour tomber sur le nombre rond, qui n’a jamais attendu qu’un réveil à chiffres affiche l’heure pile?
Le grand saut des indiens
La fin de l’histoire de la découverte du zéro est moins épique. C’est chez les Indiens qu’il réapparaît. Les Indiens n’avaient ni peur du vide ni de l’infini. Le cosmos hindou était infini et pour eux, tout avait été créé à partir du vide. Les indiens appréciaient donc le zéro. Ils passèrent d’un système grec à un système Babylonien en base 10. Nos chiffres sont des évolutions de leurs chiffres et ne méritent donc pas vraiment l’appellation de chiffres “arabes”.
C’est en 628 qu’est défini le zéro dans le traité de Brahmagupta. Il définit ce nombre comme la soustraction d’un nombre par lui-même. Les Arabes récupèrent alors ces écrits, les traduisent et importent ainsi le zéro.
Pendant ce temps, en Europe on continue à utiliser le système romain pourtant bien peu pratique pour faire des mathématiques. La peur du vide est toujours là mais grâce aux marchés, le zéro aura le dernier mot! La première étape est de retirer certaines doctrines un peu absurdes en postulant qu’Aristote n’a pas à décider ce que Dieu peut faire ou non!
Fibbonacci, un mathématicien italien, influencé par les Arabes, introduit le zéro en Europe dans son livre où il présente la fameuse suite qui porte son nom. Les marchands, ayant besoin de faire des opérations sans erreurs adoptèrent très rapidement le nouveau nombre… Le zéro est enfin arrivé en Europe!
Sources :
- “Zero : biography of a dangerous idea” de Charles Seife : LE livre grâce auquel j’ai construit ce dossier, tout simplement.
- “Histoires d’algorithmes : du caillou à la puce” de Jean-Luc Chabert : pas mal d’exemples sur le système babylonien et egyptien
- “The book of nothing : Vacuum, Voids, and the lastest ideas about the origins of the universe” de john D. Barrow : juste parcouru mais j’aime beaucoup BArrow.












Répondre à Pourquoi je kiffe la science les maths | Nicolas Tupégabet n'est pas sur l'Internet Annuler la réponse