Xavier Niel fanfaronne et annonce la création d’une école, au doux nom de la réponse à la question de l’univers et tout le reste : 42. Il n’en fallait pas plus pour m’attirer, alors…
Le premier jour, je me suis inscrit.
Le deuxième jour j’ai fait les 3 premières évaluations.
la validation de la troisième épreuve débloquait l’épreuve 4. Et c’est avec cette évaluation que les choses sérieuses commencent. En effet, déjà l’évaluation dure 4H, on est bien loin des évaluation de 10 minutes du début!
Il était 21H, jusqu’à 1H du matin et ce jour là, je subissais l’évaluation 4 de 42.
Découverte et compréhension
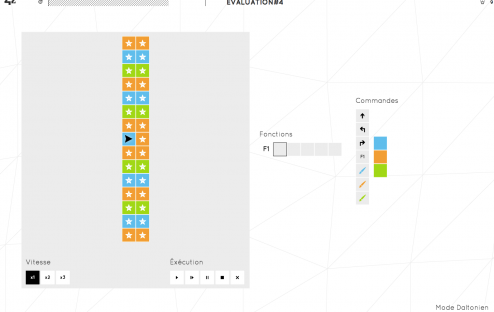
Comme dans la plupart des évaluations, on arrive sur une page épurée sans aucune explication ni consignes. Heureusement, quelques boutons connus culturellement : un bouton play, pause, stop, une croix.
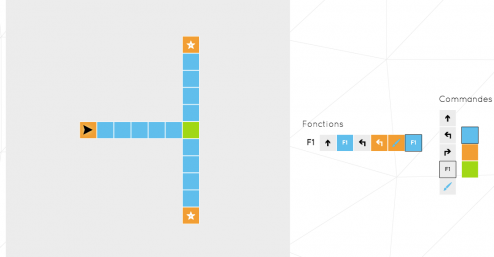
Le premier réflexe est d’appuyer sur play. Et là, il ne se passe rien. Alors, assez logiquement on se met à cliquer partout. Une flèche, une étoile, un chemin, probablement que cette flèche doit rejoindre l’étoile. A droite, il y a une flèche vers le haut, je clique donc dessus et appuie sur play.
Se crée alors en haut de la page une “liste d’actions”.
Chaque action est executée l’une derrière l’autre. Au clic sur play, la suite d’action “F1” est lancée. On peut mettre dans F1 n’importe quelle action et l’associer à n’importe quel couleur. Mieux encore, on peut associer cette action à aucune couleur, elle sera alors exécutée quelque soit la couleur de la case sur laquelle passe la flèche (Mine de rien, comprendre tout cela m’a pris une bonne dizaine de minutes, c’est amusant un exercice sans consigne).
Reste que tout cela ne permet pas de résoudre le premier niveau de ce test. Il faut comprendre que l’on a le droit à une chose de plus : la récursivité. On peut appeler F1 dans elle même, on peut donc créer de boucles, on peut donc écrire une liste d’action qui fait avancer à l’infini notre flèche.
Notons un élément étonnant. Quand on met F1 parmi les actions, les actions de F1 sont rajoutées AU DEBUT de la liste d’action et non à la fin comme on pourrait s’y attendre.
Le premier niveau passé, l’énoncé est compris, on peut passer aux choses sérieuses.
Faire de l’informatique sans s’en rendre compte
Cette évaluation est une excellente initiation à l’informatique. En effet, très vite les exercices se complexifient et nécessitent l’utilisation de la plupart des constituantes essentiels des algorithmes. Ainsi, très vite arrive les fonctions avec une deuxième F2 voire une troisième.
Le “if” qui permet d’executer certaines fonctions dans des cas précis deviens très vite indispensable. On choisis alors des fonctions spécifiques en fonction des couleurs. 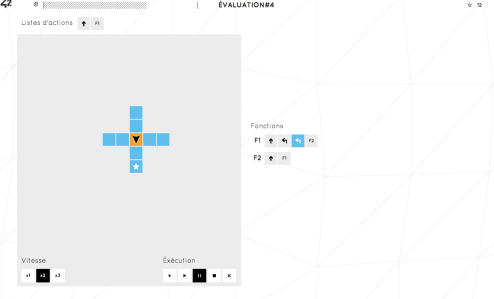
Un pinceau permet de peindre les cases ou l’on passe. Cela introduit une notion sommaire de variable.
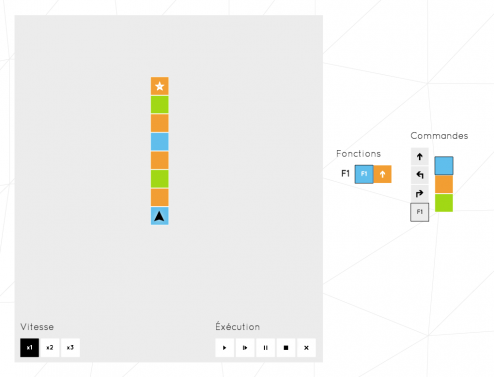
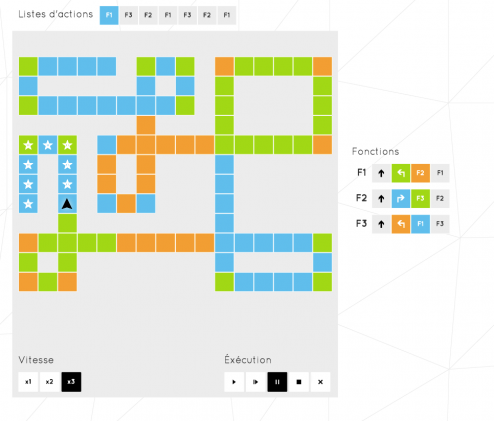
Et le mélange de toutes ces fonctions nous amène à implémenter de vrais petits automates…
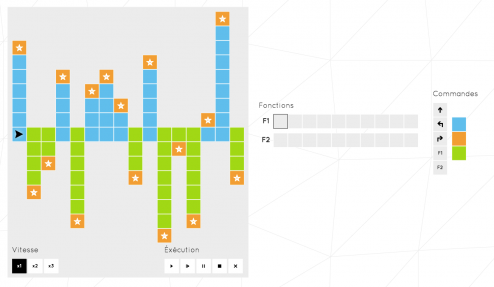
Dans le niveau ci-dessus, ma flèche avance différemment selon la couleur du sol grâce à un mélange fin de récursivité et de conditions. Elle parcours finalement un chemin très complexe, voire même anarchique grâce à trois petites fonctions.
Les niveaux nécessitent de redoubler d’ingéniosité et se répètent très peu. Les personnes qui ont conçu ces tests sont d’excellents game designers!
Game design
Cette évaluation est de loin celle ou les développeurs de 42 se sont le plus faits plaisir! Certains niveaux sont aussi beaux que complexes, en voici un florilège.
Apprentissage
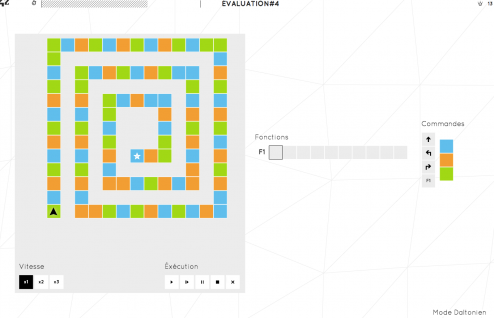
Cette merveilleuse évaluation ne se contente pas des bases, on arrive finalement à un niveau ou il va falloir prouver une nouvelle capacité : la capacité d’adaptation.
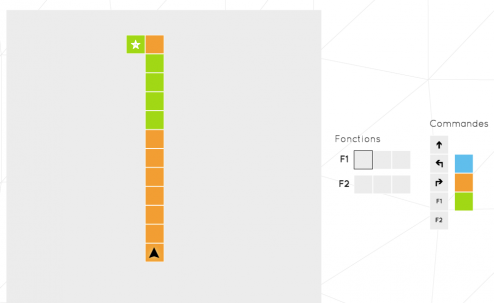
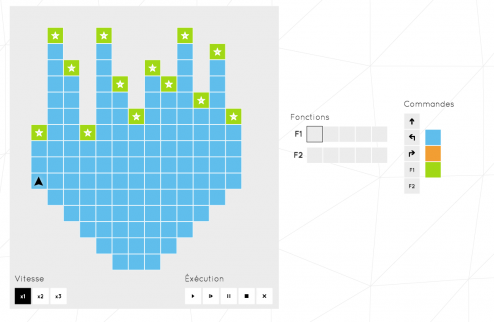
Ce niveau est particulièrement complexe car si l’outil nous fournit la récursivité et les tests simple, il ne fournit pas de variables de stockage. On ne peut donc pas mémoriser au long du parcours la longueur des chemins parcourus. Or, on observe ici des chemins de longueur très variable.
Pendant de longues minutes, cet exercice m’a paru impossible sans que je puisse le prouver (donc je n’ai bien sur pas abandonné :p). Mais c’était en oubliant un des éléments de l’exercice : la liste d’actions!
En effet, je vous ai expliqué au début de cet article, que toutes les actions d’une fonction se rajoutait à la liste d’actions puis sont exécutées l’une après l’autre. Or, imaginons, que mon action F1 soit :
F1 : ↑F2↓
Alors quand j’executerai F1, se rajouteront dans la liste d’actions respectivement Haut, F2 et bas. Puis la flèche ira vers le haut. Puis on executera F2… avant d’executer bas! Si bien qu’une action bas sera stockée en fin de chaine d’action à chaque fois que F1 sera executée.
On peut donc de cette manière compter le nombres de fois ou est executée F1 et donc redescendre d’autant de carrés que l’on est monté! Un peut de sueur et d’erreurs et l’exercice est résolu!
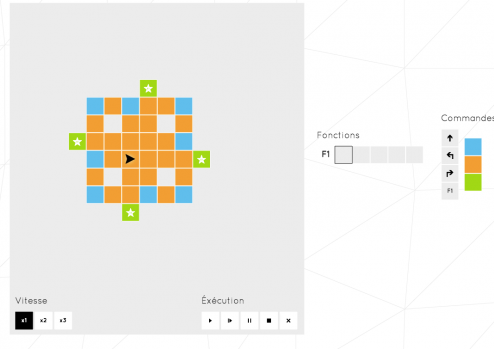
La résolution de ce test m’amène finalement au dernier test de la séance.
Attention, ce n’est pas forcément le dernier test de l’évaluation. C’est celui qui a eu raison de moi! Un peu plus d’une heure dessus et je n’en suis pas venu à bout… Si vous avez des idées, les commentaires sont là pour ça!
Et sinon à très vite pour la dernière évaluation de sélection à 42!
[EDIT] La dernière évaluation est en ligne!
Laisser un commentaire