Xavier Niel fanfaronne et annonce la création d’une école, au doux nom de la réponse à la question de l’univers et tout le reste : 42. Il n’en fallait pas plus pour m’attirer, alors…

La validation de la quatrième épreuve débloquait la toute dernière évaluation. Cette évaluation est de loin la plus intéressante a mon goût. Il est annoncé qu’elle dure deux heures.

Rencontre

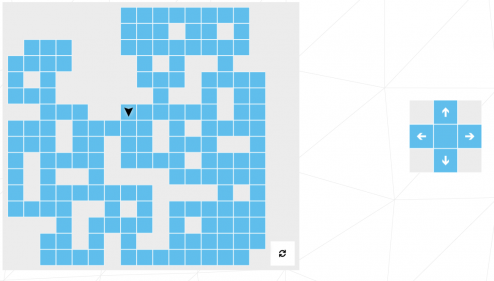
Comme la plupart des épreuves, on arrive sur un écran sans aucune instructions mais ici la règle se révèle très simple.

On a un curseur, on le controle avec les flèches. A chaque fois qu’il passe sur une case, il l’a détruit. Le but est de détruire toutes les cases.

Les game-designer de cette épreuve se sont encore éclatés et très vite ça se corse (du moins visuellement).

En fait, ce n’est pas si difficile. En s’y reprenant à deux trois fois, on viens toujours au bout, du moins presque, comme on va rapidement le voir mais d’abord un peu de math!

Les ponts de Königsberg

Ce problème est en fait extrêmement classique en théorie des graphes : il s’agit de parcourir toutes les connexions une et une seule fois.

Tout commence à Königsberg, une ville constituée de 7 ponts. Léonard Euler, en visite dans cette ville se demande s’il est possible de passer par les 7 ponts en ne parcourant chaque pont qu’une seule fois. N’hésitez pas à vous y essayer sur la carte de la ville ci-dessous.

(Image Wikimedia)

Ce problème parait tout simple et pourtant, je vous offre tout simplement une bouteille de champagne si vous le réussissez (ne pariez jamais avec un mathématicien).

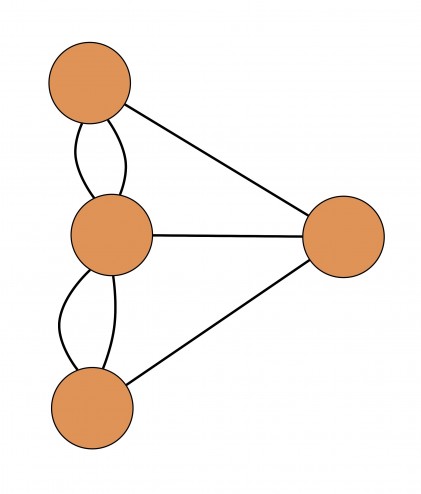
En théorie des graphe, on représenterai la ville de la sorte :

Chaque rond orangé représente une partie de la ville et les traits noirs les 7 ponts de la ville. Euler voulait parcourir la ville sans revenir sur ses pas et quoi qu’on puisse dire, son parcours aura un début et une fin (propriété extrêmement importante).

Mais oublions pour le moment cette histoire de début et de fin et plaçons nous au milieu du parcours. A chaque fois qu’Euler arrive dans une des parties de la ville (les cercles oranges), il proviens d’un pont et se dirige vers un autre pont. Ainsi, si les morceaux de ville sont au milieu du parcours, il y aura un nombre pairs de ponts qui seront parcourus autour d’eux (celui dont on viens et celui où on va, plusieurs fois si l’on passe plusieurs fois par ce morceau de ville).

Au départ et à l’arrivée par contre c’est différent. A l’arrivée, on proviens d’un pont mais on s’arrête, on ne parcourra plus de ponts. De ce fait, le nombre de ponts parcourus autour de ce morceau de ville sera impair : Le nombre pairs de ponts parcourus dans un morceau de ville au milieu de parcours plus le pont final. Au départ, même chose, un nombre impair de pont parcourus : celui de démarrage et ceux du milieu du parcours.

Revenons en à notre propriété fondamentale d’un parcours : Il n’y a qu’un départ et une arrivée. De ce fait, il ne peut y avoir qu’exactement deux morceau de ville autour desquels il y a un nombre impair de ponts, on ne peut donc pas parcourir les 7 ponts de Königsberg sur un seul parcours en ne passant qu’une fois sur chaque pont!

Remarquez qu’on peut aussi réussir ce type de parcours si tous les points ont un nombre pair de liaisons entre eux, il suffit que le départ et l’arrivée soient au même endroit.

Un problème insoluble

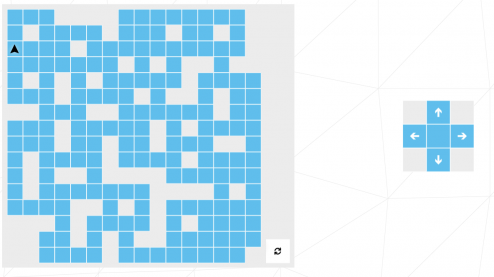
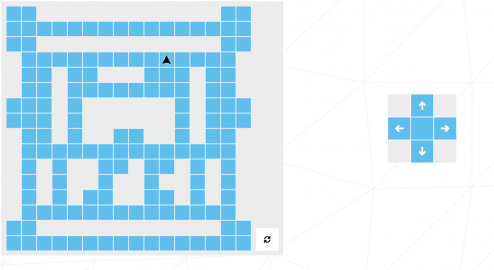
La démonstration ci-dessus permet de trouver des cas impossibles (mais en aucun cas de prouver que les autres cas sont possible même si dans les faits, il le sont). Et justement, le dernier niveau de l’évaluation de 42 est celui ci (le début est imposé, il est là ou est la flèche noire) :

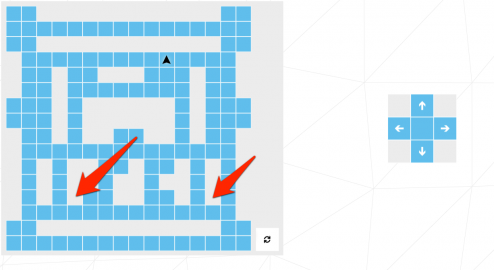
Vous reconnaissez le cas similaire aux ponts de Königsberg? On a sur cette figure deux points avec un nombre impair de liaison dont aucune n’est le départ :

L’exercice est donc impossible! Impossible du moins dans le monde de la rigueur et des règles respectées qu’est le monde mathématique mais qu’en est-il en informatique?

Become a hacker

A ce stade de l’épreuve, j’avais commencé depuis 20 minutes environ et il me restait donc théoriquement 1H40 d’épreuve. Connaissant la joyeuse ville aux 7 ponts, j’ai rapidement compris que la chose est impossible.

Me voila donc un peu perplexe 80 minutes encore devant une épreuve impossible. Il y avait deux possibilités en fait :

Les créateurs de cette épreuve sont des branques et ont même pas remarqué que c’était impossible
Ca fait parti du test.

Etant donné le talent de game designer des auteurs des épreuves, il parait très rapidement plus raisonnable de penser qu’on est dans la deuxième option. Je passe alors de l’autre coté de la matrice en demandant le code source de la page!

Et là, quelle ne fut pas ma surprise, dans ce code source, un passage où il est presque écrit en toutes lettres « Piratez moi! » (c’est une métaphore) :

function onfontload() { $('#loading').remove(); (new window.Willpower1({"map":
"[1 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,1 ,1 ,
1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,
1 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,1 ,1 ,
0 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,145 ,1 ,1 ,1 ,1 ,0 ,
0 ,1 ,1 ,0 ,1 ,1 ,0 ,0 ,0 ,1 ,1 ,1 ,0 ,1 ,1 ,0 ,
0 ,1 ,1 ,0 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,0 ,1 ,1 ,0 ,
1 ,1 ,1 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,1 ,0 ,1 ,1 ,1 ,
1 ,1 ,1 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,1 ,0 ,1 ,1 ,1 ,
0 ,1 ,1 ,0 ,1 ,0 ,0 ,1 ,1 ,0 ,0 ,1 ,0 ,1 ,1 ,0 ,
0 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,0 ,
0 ,1 ,0 ,1 ,0 ,0 ,1 ,1 ,0 ,1 ,1 ,0 ,1 ,0 ,1 ,0 ,
0 ,1 ,0 ,1 ,0 ,0 ,1 ,0 ,0 ,1 ,0 ,0 ,1 ,0 ,1 ,0 ,
0 ,1 ,0 ,1 ,0 ,1 ,1 ,0 ,0 ,1 ,1 ,0 ,1 ,0 ,1 ,0 ,
0 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,0 ,
1 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,1 ,1 ,
1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1 ,1]",
"boardwidth":"16","seed":"224754","score":"29","current_level":"5"})).Display('container');

Ca ne parait peut être pas clair à tout le monde (on est pas obligé de connaitre le javascript, personnellement je ne le connais pas!) mais bon, on a une page ou il y a une grille avec des cases bleues ou des cases transparentes et il se trouve qu’on a dans cette partie de code des 0 et des 1 qui correspondent respectivement aux cases transparentes et aux cases bleues… Avec une petite subtilité, un discret « 145 » indique la position de départ.

Google offre dans Chrome des « outils pour les développeurs » qui permettent d’executer dans la page du javascript, je décide alors d’executer le code suivant :

function onfontload() { $('#loading').remove(); (new window.Willpower1({"map":
"[145 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,
0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0]",
"boardwidth":"16","seed":"224754","score":"29","current_level":"5"})).Display('container');

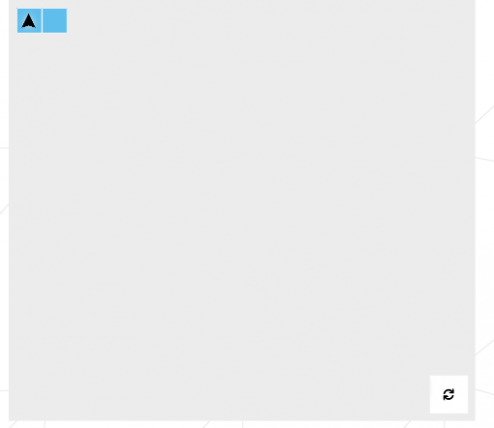
Et hop! Me voila avec un niveau bien plus facile que le précédent :

Autant vous dire qu’à ce stade j’ai réussi l’épreuve qui se trouvait être la dernière.

Conclusion

Je trouve cette épreuve tout à fait excellent. D’abord il faut avoir suffisamment de recul pour envisager qu’un test soit impossible et s’en convaincre par un semblant de démonstration. Ensuite il ne faut pas s’avouer vaincu et faire preuve de curiosité Finalement, il ne faut pas hésiter à chercher dans google comment « hacker » la page. Autant de qualité qu’il faudra à un futur informaticien.

Il m’a fallu trente minutes pour réussir le test parce que j’avais des connaissance en informatique mais je suis sûr qu’en deux heures avec l’aide de Google on peut en venir à bout.

Voila, j’ai fini les évaluation de 42 et ai appris il y a peu que j’étais admissible pour la suite. La prochaine étape est un oral, à suivre…