Le grand mathématicien Klein, après avoir obtenu la plus prestigieuse marque de reconnaissance allemande, le “Geheimrat”, insistait toujours pour se faire appeler par ce titre. Comment donc Hilbert, dont nous allons parler dans ce dossier, préférait lui se faire appeler? un de ses anciens étudiants répondit simplement : “Hilbert ? Il s’en fichait. Il était le roi. Il était Hilbert.”

En effet de son vivant, Hilbert était déja connu, il était même déjà une légende et aujourd’hui encore il fait parti des plus grands mathématiciens de l’histoire. On va tâcher dans ce dossier de comprendre pourquoi.

Je vais avoir du mal à vous parler de tout ce qu’a fait Hilbert mais on va tâcher de présenter quelques uns de ses travaux au fil desquels j’espère que vous apréhenderez mieux le personnage. Hilbert est né en 1862, il enseigne d’abord à Koninsberg puis à Gottingen où il finira sa carrière. C’est dès ses 28 ans qu’il publie son premier résultat important, la résolution du problème de Gordan en théorie des invariants.

Problème de Gordan

En mathématique, une fois un repère défini, on utilise souvent une équation pour représenter une courbe. Si l’on change de repère, l’équation change alors que l’on a toujours à faire à la même courbe. La théorie des invariants consiste justement à étudier ce qui ne change pas en changeant de repère, les caractéristiques propres de la courbe en somme. En 1868, Gordan montre un premier résultat important dans ce domaine et pendant 20 ans, personne ne parviens à aller plus loin jusqu’à ce qu’Hilbert publie ses résultats. Si le résultat fait polémique à l’époque, ce n’est pas tant pour son résultat que je ne détaillerai pas ici (et qui vaudra plutôt à Hilbert d’entrer de manière fracassante sur la scène mathématique) mais plutôt pour l’originalité que prend ce résultat.

En effet car bien que son travaille démontre l’existance d’une solution à un problème bien précis, il ne donne aucun moyen de trouver, de fabriquer, cette solution. C’est une démonstration d’existence pure tels seuls les mathématiciens ont le secret : “C’est possible, je l’ai démontré, mais je n’ai aucune idée de comment faire dans la pratique!”.

Gordan, qui a donné son nom au problème, annonce même que “ce n’est pas des mathématiques mais de la théologie!”. Les débats ne durent pas longtemps car trois ans plus tard, il trouve une preuve qui permet de construire la solution, tout le monde est donc content.

Dans sa preuve « non constructiviste”, Hilbert étudie en fait les choses de manière très générale, très abstraites. Il prend un jeu d’hypothèses, certes respectées par les invariants mais aussi par plein d’autres objets et on n’a finalement pas besoin de préciser ce qu’ils sont et il en déduit des propriétés dont celle finalement qui fait le sujet de l’article. En fait, sa théorie est beaucoup plus générale et le résultat sur les invariants n’en est qu’une petite partie, tellement annexe qu’elle ne porte pas le nom de théorème mais de « lemme ».

En mathématique, il y a une sorte de hiérarchie des résultats. Quand vous êtres très fier d’un résultat et qu’il vous a demandé beaucoup de travail, vous appelez ça un théorème. Ce que vous déduisez directement d’un théorème, vous appelez ça un corollaire. Enfin, un résultat intermédiaire, le plus souvent technique et/ou pas passionnant, on appelle ça un lemme…

Cette perspective abstraite et l’article suivant donnant une construction marquent la fin des principaux résultats de la théorie des invariants et ouvrent le nouveau domaine de l’étude de ces objets abstrait dont les invariants sont un exemple parmi d’autres. Hilbert conclut alors que “les buts les plus importants de la théorie concernée par les invariants ont été atteints” et annonce qu’il quitte définitivement la théorie des invariants… veni vidi vici!

Mine de rien, ce premier résultat important porte déjà la plupart des marques de Hilbert. D’abord son coté “bulldozer”, à savoir qu’il s’intéresse à un domaine et résout tout ce qu’il y avait à résoudre. Ensuite, sa résolution ouvre, comme souvent, nombre de nouvelles questions et champs mathématiques. Enfin, il raisonne en toute abstraction, sans forcément nécessiter un certain lien avec le “réel”.

Axiomatisation de la géométrie

Hilbert a donc quitté les invariants mais n’en a pas finit avec l’abstraction et part donc se rendre utile dans un autre domaine. Il s’attaque à l’axiomatisation de la géométrie. Pour vous replacer le sujet, les axiomes de la géométrie ont été définis par Euclide au 300e sciècle avant notre ère et n’ont plus trop été touchés depuis. Mais maintenant, au XIXe siècle, les axiomes d’Euclides ne sont pas assez précis et ont besoin d’un coup de jeune, c’est exactement ce que va faire Hilbert dans ses “Fondements de la géométrie”.

Son travail dans ce domaine est très bien illustré par une anecdote qu’il fit à ses élèves : “On devrait pouvoir parler en géométrie de tables, de chaises et de chopes de bière, au lieu de points, de droites et de plans”. En somme, Hilbert ne s’intéressent pas à ce que sont les objets “droite” et “plan”, il s’intéresse seulement aux propriétés qu’ils respectent. Le fait de savoir s’ils “existent”, s’ils sont représentatifs de notre monde ne l’intéresse pas pour construire son axiomatique. Il se contente alors pour seule définition :
“Nous pensons trois systèmes différents de choses. Nous nommons les choses du premier système les points […]. Nous nommons droites les choses du deuxième système […]. Nous appelons plans les choses du troisième système. […].
Entre les points, les droites et les plans, nous imaginons certaines relations que nous exprimons par des expressions telles que ”être sur“, ”entre“, ”congruent“. La description exacte et appropriée au but des mathématiques de ces relations est donnée par les axiomes de la géométrie”.

Il n’a donc pas besoin de savoir ce qu’est un “point” et ce que veut dire “être sur” pour définir et démontrer les éléments de sa géométrie, il lui suffit de supposer un certain nombre de propriétés entre objets et relations. Cela tranche tout particulièrement avec Euclide qui définit d’abord point et droite avant de poser ses axiomes. Les axiomes d’Euclide ne conviennent plus aux mathématiciens de cette époque, en particulier, ils acceptent mal l’axiome des parallèles, qui affirme que par un point extérieur à une droite, ne passe qu’une droite parallèle. Cet axiome parait bien compliqué au regard des autres et beaucoup sont persuadés qu’il découle des autres. En cherchant à démontrer qu’une géométrie ou cet axiome est faux est absurde, ils se retrouvent à créer des géométries certes étranges mais tout à fait cohérentes. Pire encore, Klein parviens à établir une construction qui démontre que s’il existe une incohérence dans sa géométrie non euclidienne, on peut trouver une incohérence similaire dans la géométrie euclidienne : aucune des deux n’est plus cohérente que l’autre!

Les deux types de géométries étant parfaitement cohérentes, on cherche alors à établir un lien avec la “réalité”, à savoir si le monde dans lequel nous vivons est euclidien ou non euclidien et arriver à cela, il faut reformuler les axiomes d’Euclide de manière plus simple et surtout par des formulations vérifiables par l’expérience. Comme pour les invariants, Hilbert prend une direction opposée, il cherche lui à séparer l’axiomatique de l’expérience!

Le fait de rendre plus “abstraite” cette géométrie a des conséquences essentielles. Si l’on prend par exemple la géométrie euclidienne que nous avons tous connu à l’école et qu’on lui ajoute quelques objets qui nous permettent de faire des mesures, on peut faire l’expérience suivante. Prenez une droite et un point. On peut chercher le point de la droite le plus proche de notre point. Et ce n’est pas qu’un délire de matheux, imaginez que vous n’ayiez le droit qu’aux points de la droite et que vous vouliez pourant représenter le point, vous allez chercher à faire au mieux, à trouver le point le moins différent. En fait ce point de la droite le plus proche du point extérieur est le projeté orthogonal, c’est à dire le point de la droite qui va permettre de former un angle droit.

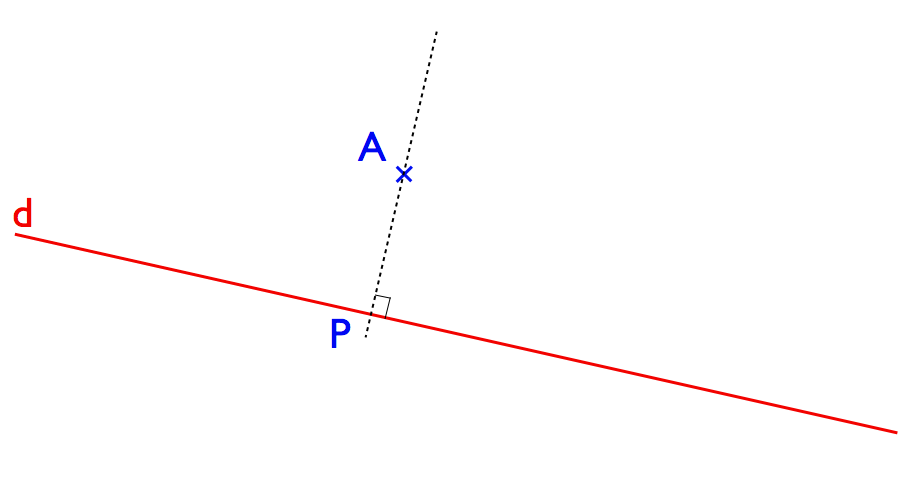
Alors jusqu’ici rien d’extraordinaire, vous l’auriez fait de vous même. Ce qu’apporte Hilbert à cet époque est en somme de dire que tout cela ne fonctionne pas qu’avec les “points” et “droites” usuels mais que l’on peut faire les mêmes choses avec tout objet qui respectent les mêmes propriétés. Rappelez vous mon dossier sur la transformée de Fourier. On avait des images, que l’on va appeler “points” et on cherchait à représenter cette image avec des rayures. Un type de rayures forme alors une droite et selon la position où l’on est sur la droite les rayures sont plus ou moins contrastées. Trouver l’image de rayures la plus proche de l’image de départ ne consiste à rien d’autre que faire la même opération : une projection orthogonale! La transformée de Fourier n’est rien d’autre qu’une projection orthogonale où les points seraient des fonctions et l’espace sur lequel on projette, un ensemble de fonctions bien particulières, les sinus et cosinus. Et pour avoir le droit de dire ça, il suffit de vérifier que l’on respecte bien les quelques axiomes.

Du coup, les géométries diverses et variées sont utilisées dans pratiquement tous les domaines scientifiques. La relativité par exemple se fait sur des espaces non euclidiens et ce n’est pas si étonnant quand on sait que Hilbert a développé une théorie similaire à la relativité au même moment et indépendamment d’Einstein. Hilbert néanmoins admettait sans problème qu’Einstein avait eu la meilleur approche, et que cela était sans doute du au fait qu’Einstein “n’avait jamais rien appris sur les mathématique du temps et de l’espace avant!”

Consistance, indépendance et complétude

Poser un jeu d’axiome est bien joli mais finalement sans rapport à la réalité, on pourrait croire qu’on fait ce que l’on veut et ce n’est bien sur pas le cas. Après avoir posé ses axiomes, Hilbert a travaillé à montrer leur non-contradiction. C’est à dire à prouver qu’il est impossible avec ces propriétés d’écrire une proposition contradictoire. Ce n’est pas un détail, car si on trouve un jour dans une théorie mathématique une contradiction, c’est toute la théorie qui s’effondre! Car à partir d’une simple contradiction, il est possible de prouver n’importe quoi… et son contraire. Il faut aussi montrer l’indépendance des axiomes, c’est à dire qu’on ne peut pas déduire un axiome donné des autres. Cette propriété n’est pas indispensable pour peu que l’on ai montré la non-contradiction mais des axiomes non indépendant voudrait dire qu’on en fait plus que le nécessaire et n’oubliez jamais que les matheux sont des flemmards!

Avec Hilbert, un axiome n’est plus vrai car il traduit l’expérience mais car il s’inscrit dans un système consistant. Cela marque le début des mathématiques modernes et marque aussi un point de rupture avec les autres sciences dont on a souvent eu l’occasion de discuter ici. Ce changement a aussi une autre implication, en tuant le lien avec l’expérience, le problème de l’axiomatisation deviens un problème mathématique et, au même titre que les autres problèmes mathématiques, il pourra être étudié et mener à des démonstrations tel que le théorème de Gôdel dont nous allons reparler tout de suite.

Cette tâche sur les fondements de la géométrie n’est qu’un début d’une plus grande mission menée par Hilbert, le programme formaliste. Ce qui marque le début de cette nouvelle période est la découverte de paradoxes. Les paradoxes en mathématiques sont plus “graves” que dans bien d’autres sciences, ce sont des contradictions et, comme nous l’avons vu, une simple contradiction peut détruire la théorie. En physique, un paradoxe est une expérience non vérifiée par la théorie, il montre les limites de la théorie mais ne remet généralement pas en cause les résultats précédents : si ces expériences collaient avec la théorie par le passé, ça n’a pas de raison de changer maintenant que l’on a découvert une nouvelle expérience. Ainsi, la mécanique classique modélise toujours bien les mouvements des objets à faible vitesse même maintenant qu’on sait qu’elle modélise très mal les mouvements des corps à vitesse très proche de la vitesse de la lumière.

Parmi les paradoxes exprimés à cette époque (il y en a 3), le plus connu et le plus simple est celui de Russel. Il consiste simplement à considérer E, l’ensemble des ensembles qui ne se contiennent pas. Si E n’est pas contenu dans E, alors il est un ensemble qui ne se contient pas, donc nécessairement E n’appartient pas à lui-même. Or si E n’appartient pas à lui même, alors par définition E est dans E. C’est le moment où l’on commence à avoir mal à la tête, c’est normal, c’est un paradoxe logique et notre cerveau est fait pour interpréter la logique. On le connaît aussi sous le nom de paradoxe du menteur et il apparait même dans le jeu Portal 2.

Au dela même de l’axiomatique, ce paradoxe met en question toute la démarche mathématique. En effet, il convient de comprendre où tout cela cloche. A-t-on le droit de définir cet espace E? Si l’on a pas le droit, du fait de quelle propriété? Qu’à cela ne tienne, Hilbert à montré la direction avec son axiomatisation de la géométrie, il “suffit” d’axiomatiser les mathématiques, c’est le programme formaliste dont les prémisses sont énoncées dans une conférence célèbre en 1900. C’est dans cette conférence qu’Hilbert présente aussi l’avenir des mathématiques avec 23 problèmes qui doivent être résolus pour faire avancer cette science.

La guerre du fondement des mathématiques

Axiomatiser les mathématiques n’est pas une mince affaire, il consiste donc à définir tous les termes et relations que nous serons amenés à utiliser. Puis de donner des règles de déduction, et, histoire de ne pas perdre toute une histoire des mathématiques, tacher de faire cela en arrivant finalement à redémontrer tous les résultats existants mais en éliminant les contradictions…. rien que ça!

Deux grandes théories sont “touchées” par les paradoxes. La première n’est rien de moins que l’arithmétique (c’est la théorie qui permet de faire des aditions, des multiplications, etc.). Le problème avec l’arithmétique est que la théorie est la plus simple connue et donc est utilisée dans beaucoup d’autres. En particulier, Hilbert démontre que la consistance de son système de géométrie est équivalente à la consistance de l’arithmétique, on se doute bien alors qu’il ne pourra pas prouver la consistance de l’arithmétique par la même méthode…

la seconde est la théorie des ensembles de Cantor dont nous avons déjà parlé dans l’épisode sur l’infini et qui permet d’aboutir au paradoxe de Russel. Beaucoup des mathématiciens de l’époque n’appreciaient déjà pas cette théorie pour le moins étrange et ce genre de paradoxe n’arrangea rien et pousse à la naissance de l’intuitionisme. Les intuitionistes considèrent que cette théorie et ces paradoxes qui en découlent sont du à une utilisation abusive de logique abstraite qui pousse à une perte totale de sens. Ils proposent alors de se limiter à une logique dans laquelle on peut construire les objets, typiquement dans laquelle la preuve d’existance sans construction de Hilbert n’est pas une preuve. Ils refusent à titre d’exemple le principe du tiers exclu qui affirme qu’une proposition ou son contraire est vraie. Exclure le tiers exclu veut donc dire que l’on accepte que dans certain cas ni la proposition ni son contraire n’est vraie. C’est ce principe qui permet d’amener à beaucoup de preuves sans construction Rappelez-vous par exemple le dossier sur les algorithmes, on a démontré que tous les nombres réells ne sont pas calculables par un ordinateur. Grâce au tiers exclu, on peut en déduire qu’il existe un nombre non calculable par un ordinateur sans pour autant être capable de le construire! Finalement, la logique intuitioniste est sans doute la partie des mathématiques la plus facilement comprise/acceptée car se contraignant à chaque étape de pouvoir effectivement fabriquer les objets.

Mais comme on le voit ici, cette logique est plus restreinte que celle utilisée jusqu’alors et amène à se séparer de beaucoup de belles théories. En particulier, dans un monde intuitioniste, il faudrait dire au revoir à la théorie de Cantor, ce à quoi Hilbert s’oppose en affirmant le célèbre : “Nul ne doit nous exclure du Paradis que Cantor a créé”

La guerre est donc lancée et à l’époque c’est mal parti pour Hilbert et les formalistes, en effet, leur utilisation intensive de la logique amène à des paradoxes qui pourrait être évités en se limitant au programme intuitioniste.

Le programme formaliste

Hilbert, Bernays et Ackermann reprennent alors les bases et ils commencent par l’arithmétique la plus simple. ils commencent avec un signe | (vous pouvez appeler ça 1 si vous voulez), définissent l’addition, montrent des résultats en supposant des axiomes mais dans un premier temps restent dans une approche bien palpable : ils s’interdisent d’utiliser l’infini et tâchent à ce que chaque démonstration soit réalisable par une expérience. Cela veut dire par exemple qu’il s’interdisent de jouer avec l’ensemble de tous les nombres, car ils auront bien du mal à réaliser une expérience avec une infinité de termes. Cette première mathématique est appelée mathématique contentuelle et est en fait plus restreinte encore que l’intuitionisme et comme elle est basée sur l’expérience, elle parait évidente.

Sur cette base, les formalistes tachent alors d’intégrer les autres théories en s’autorisant une logique plus abstraite mais leur but est d’essayer de prouver, grâce aux mathématiques contentuelles que ce nouvel ensemble d’axiome est cohérent. Ils aimeraient aussi parvenir à construire un système complet, c’est à dire ou toute proposition (ou son contraire) peut être prouvée.

Ce programme aboutira finalement à un échec caractérisé par le théorème de Gödel, déjà vu dans le dossier de Robin. Godel tue tout espoir de parvenir à un tel résultat, avec une approche formaliste ou non. Il élimine aussi l’espoir des intuitionistes. En effet, Godel arrive à montrer que la théorie intuitioniste est parfaitement équivalente à l’arithmétique classique, si bien que contrairement aux apparences, les restrictions des intuitionistes ne permettent pas de rendre plus cohérente la théorie arithmétique, elles ne changent rien.

Au niveau formaliste, Gödel montre que l’on ne peut pas prouver la consistance d’une théorie au sein même de cette théorie, ainsi, le programme formalisme qui voulait justement parvenir à ce résultat est voué à l’échec. Le programme reste malgré tout important, d’abord Gödel s’est probablement interessé au sujet pour résoudre les questions du programme. Ensuite l’idée du formalisme reste importante et impregne encore aujourd’hui la pratique des mathématiques : les choses dont parle les mathématiques sont des symboles vides de sens, tant que vous savez comment les manipuler, cela vous suffit pour faire des mathématiques. Il n’a finalement qu’été prouvé qu’il fallait sortir de la sphère des mathématiques pour poser convenablement ses fondements.

Mais aussi…

Hilbert ne s’est pas qu’intéressé aux maths. Il se tourne vers la physique dès 1912 pour présenter une théorie cinétique des gaz. Il considère qu’il faut faire une axiomatisation de la physique et pense que cela dit être fait par un mathématicien car il pense que maintenant “la physique est trop difficile pour des physiciens”. Ici comme souvent, il n’invente quelque chose de fondamentalement nouveau mais le simplifie et unifie plusieurs théorie utilisées à l’époque dans l’esprit d’une phrase qu’il prononça dans sa conférence de 1900 : “Une théorie mathématique n’est pas terminée tant qu’on ne l’a pas rendue si claire que l’on puisse l’expliquer à la première personne qui passe dans la rue!”. Il n’hésite pas non plus à dire qu’après avoir réformé les mathématiques, il s’attaque à la physique et quand il en aura fini il s’attaquera à la chimie qui à l’époque était, selon ses mots, “comme faire de la cuisine dans une école pour filles”. Comme nous l’avons déjà vu, en 1915, il produira une théorie de la relativité et il a eu une influence indirecte déterminante pour l’essor de la mécanique quantique. Il se trouve que les outils mathématiques de la mécanique quantique sont une application directe de la théorie des équations intégrales.s Pour autant, commençant à être âgé, il comprenait difficilement la mécanique quantique, expliquée par son assistant. Il dit un jour : “Je ne vois pas comment quelqu’un peut comprendre quelque chose à ce que se passe en physique ces jours. Même moi ne comprend tout ce que je voudrais dans les livres de physique. Et encore, quand c’est moi, si je ne comprend pas, je passe un coup de téléphone à Debye ou Born et ils m’expliquent…”.

Hilbert passera la plus grande partie de sa vie à l’université de Göttingen qui devint alors un des plus grand centres de la pensée mathématique au monde. Les meilleurs étudiants du monde étaient vivement conseillés de faire leur bagages et rejoindre cette université. Hilbert expérimentait durant ses présentations, plusieurs de ses élèves ont vu ses théories se construire au fil des cours, ils avaient l’impression de vivre la science en train de se faire (expression chère au Palais de la Dévouverte). Cet univers de réflexion et de découvertes mathématiques a imprégné élèves et professeurs et quand est arrivée la seconde guerre mondiale, la plupart, sauf Hilbert, ont du fuir l’université. Bien qu’ayant toujours refusé de faire une autre distinction entre personnes que le talent mathématique, Hilbert tenait à rester dans sa ville. Il a alors fini sa vie pratiquement seul pendant que ses anciens collègues et étudiants vivaient aux quatre coins du monde et diffusaient la pensée Hilbertienne dont tout mathématicien aujourd’hui porte un héritage.

Bibliographie

Pour préparer ce dossier, je me suis principalement aidé des deux livres suivants. A part ça n’hésitez pas à consulter les pages wikipedia dédiées à Hilbert et ses travaux dans la version anglaise de l’encyclopédie, elles sont très complètes.

• « Hilbert » par Constance Reid : Livre très long qui raconte en détail la vie de Hilbert mais avec moins de détails ses résultats. Pour autant c’est le plus intéressant des deux pour ressentir l’effervescence de l’époque à Gottingen et avoir un aperçu complet sur la vie et l’oeuvre de Hilbert.
• « Hilbert » par Pierre Cassou-Noguès : Ce livre tâche d’expliquer en détail le combat qui a eu lieu entre formalisme et intuitionisme et ce qu’ont apporté les résultats de Gödel. Par contre le livre fait dans l’efficacité, ce n’est pas romancé, cela peut déplaire…

Le grand mathématicien Klein, après avoir obtenu la plus prestigieuse marque de reconnaissance allemande, le “Geheimrat”, insistait toujours pour se faire appeler par ce titre. Comment donc Hilbert, dont nous...