PS183 – La cathédrale des objets mathématiques | Nicolas Tupégabet n'est pas sur l'Internet

Ce dossier fait parti de la soirée radio dessinée de PodcastScience au CERN, allez donc aussi consulter les autres :

Les expériences scientifiques sont d’incroyables méthodes pour appréhender et prévoir le monde mais elle ne serait pas grand chose sans son outil préféré : les mathématiques et leur équations. Sisi, les scientifiques ne peuvent pas s’en passer! Et ce depuis le tout début, depuis le jour où ils inscrit 1+1=2 Enfin, ça c’est la belle histoire romancée… En réalité, s’il est certain que cette équation est connue depuis des lustres, elle n’a probablement été écrite en ces termes qu’autour du XVIe siècle, période où le symbole “=” a été inventé. Et encore, on n’utilisait le signe « + » que depuis environ un siècle… Pour les chiffres « arabes » c’est en revanche plus vieux, quelques trois millénaires AVJC, enfin sauf bien sur pour le zéro hein, qui a mis un sacré bout de temps à arriver, à être de nouveau oublié, puis à être utilisé comme on le fait aujourd’hui. Tout cela pour dire que les symboles, les outils mathématiques que l’on utilise aujourd’hui sont loin d’avoir toujours existé et sont loin d’être figés dans le temps. Leur construction a même pu prendre un temps que vous ne soupçonnez pas : ce n’est qu’après 362 pages de démonstration, au XXe sciècle, que Whithead et Russel ont finalement prouvé que 1+1=2. Résultat qu’ils ont commenté en ajoutant « cette équation peut parfois se montrer utile ». Et malgré cette évolution incessante, les équations ont toujours a peu près la même tête : des MACHINS « additionnés » ou « multipliés » avec des BIDULES qui en fait sont « égaux » à des trucs. MACHIN + BIDULE = TRUC ou MACHIN x BIDULE = TRUC Ce n’est qu’une illusion, ça fait bien longtemps que les mathématiciens n’utilisent plus vraiment les nombres, les aditions et les égalités que vous avez apprises à l’école. Comme avec toute drogue, les mathématiciens ont eu besoin d’aller plus loin en construisant des objets conceptuels délirants, bravant parfois des interdits historiques! Vous savez, ce genre d’interdits comme « celui dont on ne dit pas le nom » dans « le livre que je ne citerai pas parce qu’il est trop connu ». Ce mathématicien qui arrive un matin, transpirant, et qui vous dit : « Vous pouvez faire tout ce que vous voulez mais JAMAIS, au grand JAMAIS ne divisez par zéro« ! En fait, on vous a menti, on peut diviser par zéro, comme on peut dire Voldemort, mais cela a un prix ! Pour diviser par zéro, il faut ajouter aux nombres l’infini et bidouiller un peu pour que ça marche, en gros il faut accepter que l’infini et -l’infini c’est la même chose. Ça peut paraître étrange mais ça consiste tout bêtement a prendre la ligne des nombres et de la refermer sur elle-même pour en faire un cercle. C’est ce qu’on appelle la géométrie projective. 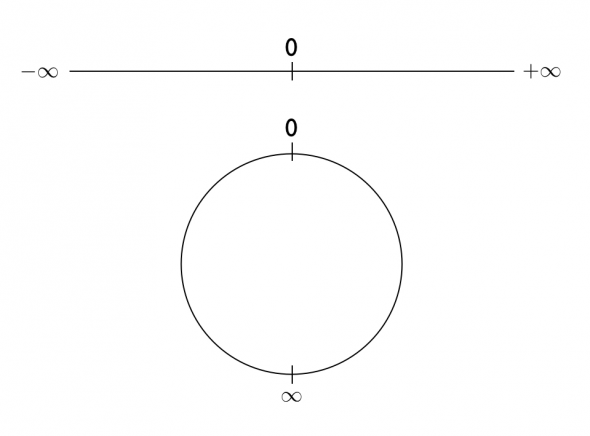Ces géométries sont un peu étranges, elles obéissent à d’autres règles du jeu. Par exemple deux droites ont toujours une intersection (donc ne parlez plus de droites parallèles ; dans cette géométrie, ça n’a aucun sens). Est-ce que c’est si bizarre? Finalement quand on regarde une route aux côtés bien parallèles, on a l’impression que les deux cotés de la route viennent se rejoindre sur un point à l’horizon. C’est pour cela que cette géométrie très étrange est très utile, elle est terriblement efficace pour tous les calculs liés à la perspective : la correction des photos façades de bâtiments prises d’en bas du bâtiment par exemple! De toute manière, la bizarrerie dépend largement du point de vue, par exemple on a dû vous apprendre à l’école que « la somme des angles d’un triangle fait 180° », eh bien en fait c’est parfois faux… enfin souvent… enfin la plupart du temps quoi! Et en particulier c’est faux en géométrie projective. Mais pas que sur ce genre d’espace un peu étrange où l’on peut diviser par zéro, c’est aussi faux sur la surface du globe. Imaginez par exemple un triangle dont les sommet sont au pôle nord, un point de l’équateur et un autre point à mi-chemin sur l’équateur entre ce point et son opposé sur le globe. On obtient un triangle avec trois angles droits!

Aujourd’hui, une des questions centrale de la cosmologie est de savoir que donne la somme des angles d’un triangle dans l’univers, 180°? un peu plus? ou un peu moins? Toutes ces possibilités correspondent à des géométries plus bizarroïdes les unes que les autres. Si cette somme est égale ou plus grande que 180 degrés, on a le choix entre une vingtaine de géométries qui respectent la relativité générale d’Einstein et si cela fait moins de 180 degrés, on a le choix parmi une infinité de géométries différentes ! Revenons à notre équation fondamentale MACHIN + BIDULE = TRUC. Un peu comme dans nos exemples de géométries biscornues et de division par zéro, le travail si mystérieux du mathématicien consiste justement à donner de nouvelles définitions à chacun des termes de ces équations et à regarder ce que cela peut donner. Par exemple définir des nouvelles « additions », « multiplications » : comment multiplier deux mouvements du Rubik’s Cube. Et surtout, définir de nouveaux MACHINS, BIDULES et TRUCS et la dessus les scientifiques de ces dernières années se sont servis avec plaisir : La mécanique quantique utilise des objets qui n’ont qu’une valeur une fois mesurés, les distributions, la théorie des cordes nous parle des objets en allant au-delà de la dimension 4, la cryptographie s’amuse à « additionner » les points de courbes particulières, les exemples sont sans fin ! Ce qui est pratique avec les outils mathématiques c’est qu’en général, ils ne respectent qu’un tout petit nombre de propriétés, de règles du jeu. Et si quoi que ce soit les respecte aussi, on a le droit d’utiliser l’intégralité des résultats démontrés parfois sur des siècles. Alors certes, cette « cathédrale » conceptuelle est moins visible que ses homologues matérielles que sont les expériences hors normes mais elle n’en est pas moins imposante tant les mathématiciens chaque jour s’attellent à en faire un seul monument unifié dont toutes les pièces communiquent. Quelques livres pour savourer les équations mathématiques :

The universe in zero word : Un bouquin qui parle de plusieurs équations et raconte les concepts mathématiques liés
17 equations that changed the world : la même chose, par Ian Stewart et pas exactement le même jeu d’équtation