Cet article est une reproduction du dossier que j’ai écrit pour Podcastscience et je vous engage à vous abonner à ce podcast. Pour les plus flemmards, le texte et l’audio dans la suite…

[audio:http://www.podcastscience.fm/podpress_trac/web/2226/0/116-transformee-fourier.mp3]

En 1799, une pierre pour le peu étonnante est découverte à Rosette. Ce simple morceau de roche contient trois inscriptions : l’une en Hiéroglyphes égyptiens anciens, la deuxième en égyptien démotique et la troisième en grec ancien. Rapidement, l’intuition universellement partagée était que les trois inscriptions étaient le même message dans les trois langues.

Encore fallait-il le prouver et surtout trouver le moyen de faire le chemin d’une langue à l’autre. C’est exactement ce que termina Champollion, un protégé de Joseph Fourier (le mathématicien dont nous allons très vite reparler), en résolvant le mystère des hiéroglyphes.

Il existe autant de systèmes de communication que de groupes d’êtres vivants qu’il pût y avoir dans l’histoire. Et en général, animaux ou humains ont contruit leur « langage » pour répondre au mieux à leurs besoins. Chaque traduction n’est alors que la transcription d’une même idée. Dans l’avant-propos de l’édition française de GEB (ce fameux livre dont je vous parle dans trois dossiers sur quatre), l’auteur (le vrai, l’anglais) qui a tenu à écrire cet avant-propos en français, raconte cela mieux que quiconque :

« Qui lira les éditions anglaise et française de GEB aura un avantage sur les lecteurs en une seule langue : en comparant deux passages, il pourra distinguer ce qui est « glissable », ou l’inessentiel, de ce qui est ferme et essentiel. Comme cela, il découvrira un noyau inglissable : le GEB « platonicien », le GEB idéal, flottant majestueusement dans un espace éthéré, indépendant de toute langue terrestre.[…] Chaque GEB concret — c’est à dire dans une langue particulière — n’est que l’ombre du GEB platonicien sur un mur particulier. »

Ce dossier propose de raconter comment la transformée de Fourier et ses développements ont offert aux sciences une infinité de langages et une méthode de traduction pour passer de l’un à l’autre.

À la découverte d’un nouveau langage

Tout comme la pierre de rosette permit de relier plusieurs langues, c’est par deux « traductions » d’un même problème que sont apparues pour la première fois les séries de Fourier, ancêtre de la transformée de Fourier. Ce problème, c’est celui de mettre en équation le mouvement d’une corde de guitare après qu’on l’ait lâchée. Ce même mouvement que l’on peut facilement observer grâce à certains smartphones…

Pour mettre en équation ce problème, on choisit de s’intéresser à l’écartement de la corde par rapport à sa position au repos tout au long de celle-ci.

Cet écartement dépend non seulement de la position sur la corde (il n’y a aucune raison que la corde ait le même écartement partout) et du temps (elle vibre!). En fait, depuis que Newton s’est pris une pomme sur la poire, on peut même affirmer que cet écartement évolue comme une onde qui se propage : les équations de Newton permettent de démontrer que la variation de l’écartement de la corde au cours du temps est directement lié à la variation de l’écartement de la corde tout au long de celle-ci.

Reste qu’il fallut trouver une solution, ce que firent D’Alembert et Euler en prouvant que les solutions de l’équation du mouvement d’une corde pouvaient s’exprimer comme la combinaison de deux fonctions périodiques. Une fonction périodique n’est pas forcément une belle vague comme on a souvent tendance à les représenter. En fait, elle peut être tout à fait n’importe quoi sur sa période pour peu que cette période justement se répète indéfiniment.

Pour autant, les mathématiques étant une science de flemmards, l’envie s’est rapidement fait sentir de raccrocher cela à quelque chose de plus simple et bien connu : les sinus et cosinus! Ces fonctions sont connues de très longue date, ont le bon goût d’être périodiques et surtout de former des solutions particulières de l’équation des cordes vibrantes. Il n’en fallut pas plus pour que Bernoulli envisage que toutes les solutions de cette équation puissent s’exprimer comme une somme infinie de sinus et cosinus bien choisis.

Mais si ces « Séries de Fourier » ne portent pas le nom de Bernoulli, c’est bien parce que cette intuition posait un problème de taille qu’il ne sut résoudre. Tout comme on était convaincu que les textes de la pierre de rosette étaient la traduction du même contenu dans différentes langues sans encore pouvoir élucider la manière pour passer d’un langage à l’autre, il restait encore à trouver comment décomposer une fonction périodique quelconque en série de Fourier. Et contrairement à la pierre égyptienne, la plupart des mathématiciens de l’époque étaient convaincus que les deux mondes ne coïncidaient pas, que certaines fonctions ne pourraient jamais être transcrites en série de Fourier. Par exemple comment réussir à reconstruire une fonction discontinue (qui nécessite de lever le crayon pour la tracer) à partir d’une somme de fonctions continues (où le crayon reste tout le long posé sur la feuille)? Les habitués du podcast savent déjà que l’infini permet beaucoup de choses étonnantes!

En 1822, quand Napoléon cessa de l’empêcher de pratiquer les mathématiques pour l’emmener en Égypte ou lui donner la charge d’une préfecture, Joseph Fourier présenta dans un article la méthode de traduction en série de Fourier.

AKOIDONCKESKESASERT?

Alors c’est bien beau de traduire une fonction mathématique dans une autre langue mathématique, mais on est loin de la promesse introductive d’une révolution scientifique… Il est donc plus que temps de détailler à quoi peut bien servir cette « transformée de Fourier » en l’état.

La plupart des mesures que nous sommes capables de faire dépendent du temps :

• Un micro mesure la force exercée par les vibrations de l’air sur sa membrane au cours du temps
• Une antenne mesure le champ magnétique et ses variations au fur et à mesure que le temps court
• Le laser du DVD, CD et Autre Blu-Ray viens mesurer la profondeur des scillons sur les disques
• etc.

Et pourtant, connaître l’évolution temporelle d’une mesure est rarement l’information la plus intéressante. L’homme est un animal qui aime les coïncidences, les schémas qui se répètent, afin de pouvoir y apposer des règles et tenter une fois de plus de prévoir l’avenir! Par exemple, pour vérifier ou non une croyance urbaine (récemment annihilée par Alan) selon laquelle la lune influence le sommeil, on aurait pu mesurer pendant plusieurs mois les ondes cérébrales des individus et regarder si l’on peut voir quelque chose se répéter avec un cycle qui aurait un quelconque rapport avec le cycle de la lune. La tâche est assez fastidieuse, le cycle de la lune étant de 29 jours, il aurait fallu essayer de trouver des liens entre les valeurs des signaux d’ondes cérébrales éloignés de 29 jours, de 58 jours (2 cycles), de 87 jours (3 cycles), etc. Ne sachant bien sur pas quelle allure de la lune influencerait le sommeil et dans quel sens. Une tâche très complexe en somme parce que l’information que l’on cherche, des répétitions selon un certain rythme, s’exprime très mal dans le monde temporel.

Un autre exemple récent et amusant a été observé à la coupe du monde de 2010. Chaque match comportait l’aussi traditionnel qu’agaçant son de la vuvuzela…

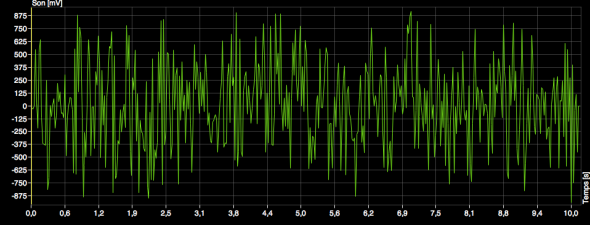
Le Vuvuzela est un instrument de musique et comme tout instrument de musique, il fait vibrer l’air de manière très régulière. Pourtant, je vous mets au défi de retrouver de la régularité dans le bordel du signal temporel de ses vibrations sonores :

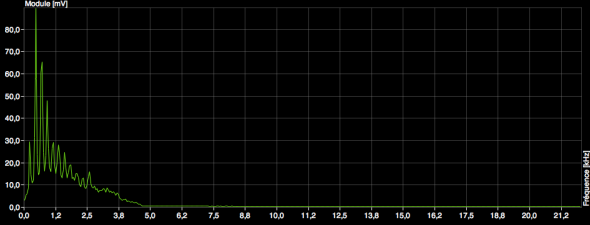
Heureusement, on connaît un autre monde, celui des fréquences! Au lieu de regarder une mesure à chaque instant, on va mesurer les répétitions présentes pour un ensemble de périodes. On va regarder les évènements qui se produisent tous les jours, tous les deux jours, et ainsi de suite. La fréquence est justement l’unité de mesure du nombre d’évènements par seconde : 1 fréquence de 1Hz concerne les signaux qui se répètent toutes les secondes alors qu’une fréquence de 10Hz ceux qui se répètent dix fois par seconde. Dans un tel monde, il est trivial de voir si la lune a une influence sur le sommeil, il suffit en effet de regarder aux alentours des fréquences multiples de 29 jours si le nombre d’évènements est plus important qu’ailleurs. Dans la représentation fréquentielle, regarder s’il y a des évènements particuliers au rythme de la lune est aussi simple que regarder la valeur du signal en un instant sur la représentation temporelle.

Par exemple, il est trivial de repérer la vuvuzela dans la décomposition fréquentielle du signal précédent, les valeurs les plus fortes se situent autour de 600Hz, avec quelques autres valeurs fortes répétées régulièrement à côté, car la vuvuzela n’est pas un instrument parfait.

Fourier a donné au monde le calcul qui permet de passer d’une représentation temporelle à une représentation fréquentielle. Il a donné à n’importe qui l’oreille absolue, la capacité de décomposer n’importe quel signal en notes. Mais attention, pas seulement, parce que les fréquences ne sont pas toujours des fréquences temporelles. Une fréquence indique seulement une répétition et elle peut être tout autre chose que temporelle. Un domaine qui par exemple utilise à outrance la transformée de Fourier est le traitement des images. Une image n’est pas un signal temporel, on prend une seule photo à un instant donné très précis. Quand on appuie sur le bouton de l’appareil photo, l’intensité lumineuse rencontrant chaque pixel est enregistrée, ce qui donne une espèce de gigantesque tableau où dans chaque case est enregistrée l’intensité lumineuse.

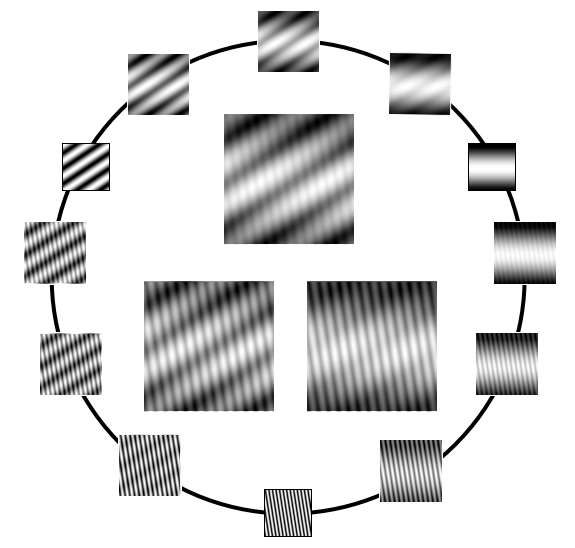
Les régularités qui seront alors susceptibles de nous intéresser ne seront pas temporelles, mais plutôt géométriques. Les images, contrairement aux signaux, ont deux dimensions : la longueur et la largeur. Chercher des répétitions dans une image consiste donc à chercher des choses qui se répètent en deux dimensions. En somme, pour faire simple, cela revient, en première approche, à rechercher des rayures. Elles peuvent avoir plusieurs orientations et être plus ou moins larges. Mais contrairement aux zèbres, on se fout pas mal de savoir si elles sont noires ou blanches! Au lieu d’utiliser les pixels pour décrire l’image, on est alors amené à utiliser les rayures.

Tout comme l’on décrit l’image en expliquant l’intensité lumineuse présente dans chaque pixel, on détaille maintenant l’image en précisant avec quelle intensité est présente chaque rayure. Si l’on reprend l’exemple de notre zèbre, les rayures verticales sont beaucoup plus présentes que les rayures horizontales.

Comme dans les langues on parle de dictionnaire : le dictionnaire des pixels et celui des rayures. La transformée de Fourier est quant à elle le dictionnaire de traduction. Et à ce jeu des traductions, certaines langues sont plus efficaces que d’autres. Ainsi alors qu’en français, on prendrait tout le temps de dire :

« Travaux préparatoires sur la contribution à la discussion du système de maintenance au soutien du matériel du système de simulation global de l’aviation pour la part nord-est de la côte artillerie de la Baltique. »

En suédois, on se contente de :

« Nordöstersjökustartilleriflygspaningssimulatoranläggningsmaterielunderhallsuppföljningssystemdiskussionsinläggsförberedelsearbeten. »

Ce qui représente une économie conséquente en nombre de lettres ou en nombre de mots. Découvrir une nouvelle langue en mathématique a directement les mêmes conséquences, d’autant plus que la langue de Fourier se révèle parfois terriblement efficace.

Prenons par exemple l’image la plus célèbre du traitement des images que vous avez pu déjà voir passer dans un Playboy des années 70. Essayons de la représenter avec une seule rayure. La moitié droite de l’image étant plus claire que la moitié gauche, la rayure qui « ressemble » le plus à Léna est une grosse rayure verticale :

Je vous accorde que la ressemblance n’est pas frappante. Mais si l’on augmente le nombre de rayures utilisées pour la représenter, on arrive très vite à reconnaître la demoiselle, et ce beaucoup plus vite qu’avec les 250 000 pixels nécessaires à la décrire…

Ces images sont bien belles, mais comment donc arrive-t-on à calculer justement à les décomposer en rayures? Comment on fait pratiquement pour « ajouter des rayures », c’est justement un des objets de la partie suivante.

Quand on découvrit qu’il n’existait pas qu’une seule langue

Parmi les caractéristiques d’un mathématicien typique, après avoir rencontré la flemmardise, il est temps de rencontrer son goût viscéral pour la généralisation. Alors quand on lui apporte une deuxième langue, il ne peut se contenter de cela. Comment pourrait-on imaginer un monde avec DEUX langues. Qu’il y en ait zéro, une ou une infinité très bien, mais sûrement pas deux! À la limite on aurait pu en vouloir Pi, mais ce n’est pas un entier.

Du coup, une fois le calcul de la transformée de connu donné par Fourier, les scientifiques sont passés par la case généralisation pour finalement exprimer cela comme un cas très particulier de quelque chose de beaucoup plus général : la projection.

Vous avez tous déjà fait une projection. La plus courante chez les non scientifiques est la projection d’ombre. Le soleil ou toute autre source lumineuse envoie ses rayons qui, ne pouvant pas nous passer à travers, laissent un morceau de mur noir, formant une ombre. L’ombre alors crée fait perdre à l’objet projeté son volume et crée parfois des choses du plus bel effet comme l’une des œuvres de Tim Noble et Sue Webster.

Dans ce cas, la projection consiste à trouver l’objet plan (une ombre) sur un mur dans une certaine direction qui est la plus proche de l’objet en volume. On perd forcément de l’information vu qu’on passe d’un objet en volume à un objet plan, mais on tâche de faire au mieux.

Pour autant, toutes les projections ne font pas perdre de l’information. Dès votre plus jeune âge, vous avez été confronté à une projection qui ne faisait pas perdre d’information : celui de la peinture! Un très grand nombre de couleurs (je suis tenté de dire infini, mais ce foutu monde réel reviendra rapidement me contredire) existent et pourtant, vos professeurs de petite section de maternelle, école primaire voire même pour certains des beaux arts ne vous ont toujours offert qu’un très petit nombre d’entre elles. Très rapidement alors, vous vous êtes sans doute rendu compte que cela ne provoquait aucune limitation, on pouvait encore obtenir toutes les couleurs possibles!

• Le magenta et le jaune mélangé à égale part donnent du vermillon (et pas de l’orange! Non, mais)
• Le cyan et le jaune font défiler une grande gamme de verts en fonction de la quantité de chacun
• Le mélange des trois couleurs permet d’obtenir de très beaux gris colorés

Bref, avec peu de couleur, en jouant sur les dosages, on peut reconstituer n’importe quelle couleur. On peut alors utiliser plusieurs « dictionnaires » qui dans ce cas seront parfois appelés palettes.

En mathématiques, cela fonctionne exactement de la même manière. Les objets d’un espace peuvent être exactement reconstruits en mélangeant avec les bons dosages les éléments d’un dictionnaire. Nos images de tout à l’heure ont été reconstruites grâce à la palette des rayures! Les intensités lumineuses se combinant à la perfection pour reconstruire l’image de départ.

Quand un dictionnaire permet de reconstruire tous les objets de l’espace, on dit qu’il est générateur de celui-ci (on parle en fait de famille génératrice pour les puristes). Et la famille des cosinus et des sinus, utilisée dans la transformée de Fourier est une famille génératrice des fonctions les plus couramment utilisées en sciences. La transformée de Fourier n’est en fait qu’une projection, l’ombre qu’aurait la fonction étudiée sur le mur des ondes et tout cela sans aucune perte!

Mais l’on peut encore pousser la comparaison avec la peinture plus loin. En avançant dans vos connaissances picturales, vous avez dû remarquer qu’il n’était pas nécessaire d’avoir des dizaines de couleurs pour les reconstruire toutes. En fait, il en suffit de 3 : le cyan, le magenta et le jaune. Toute autre couleur est inutile, car elle peut être de nouveau fabriquée avec celles-ci. En revanche, il est strictement impossible de reconstruire une couleur primaire grâce aux deux autres. Cette propriété d’une « famille » correspond à la notion de liberté en mathématique. Un dictionnaire libre n’est constitué que d’éléments indépendants. La famille de Fourier appartient aussi à ce type. Il est strictement impossible de reconstruire l’un des éléments de la famille Fourier grâce à une autre! Cette propriété donne un très grand intérêt à la transformée de Fourier. Il assure que sa décomposition est unique. Si dans le cas de la vuvuzela de tout à l’heure on détecte des éléments à 600Hz, cela ne peut pas provenir de la composition de deux autres fréquences. Tout comme si l’on utilise uniquement les trois couleurs primaires, un vermillon ne pourra provenir que du mélange du magenta et du cyan. Alors certes, le dictionnaire de Fourier là est un peu particulier parce qu’il est infini, mais on ne va pas s’arrêter à un si petit détail!

Quand on utilise un dictionnaire à la fois libre et générateur pour reconstruire un espace on parle de base. Les bases sont particulièrement intéressantes, car comme nous l’avons vu, elles permettent de décrire exactement tous les éléments étudiés (elles sont génératrices) et de manière unique (elles sont libres).

Vous devez commencer à me voir venir, les bases sont des outils pour décrire n’importe quoi et il en existe une infinité. La transformée de Fourier est la projection d’un signal, d’une image, plus généralement d’une fonction sur le dictionnaire libre et générateur des ondes. Il se prête bien à l’étude des répétitions, mais ne se prête pas à tout et chaque base peut avoir une utilité :

• Pour compresser des visages, on utilise des dictionnaires de visages (pas forcément libres en fait) comprenant des sortes de schémas de caractéristiques des visages
• Pour améliorer la qualité du scan d’une bande dessinée, on sera amené à décomposer cette image en aplat de couleurs. La famille des aplats de couleurs étant plus adaptée à ces dessins souvent plus simples que les photos.
• Les vidéos que vous regardez sont exprimés dans une famille de mini-vidéos où quelques contours se déplacent. Cela est particulièrement adapté à des vidéos où des personnages se déplacent sur le même fond,
• etc.

Les possibilités sont infinies et l’on peut construire des bases adaptées à son besoin. La seule limite étant le temps mis pour traduire le message d’un dictionnaire à un autre. Limite? Seulement jusqu’au chapitre suivant.

La création du babel fish

Des découvertes aussi importantes et utiles que la transformée de Fourier sont légion dans l’histoire des sciences et cela ne suffit pas à démocratiser son utilisation.

Pour une image de 1 300 000 pixels (c’est le nombre de pixels du type d’écran le plus répandu), il faut un million de millions d’opérations pour calculer la transformée de Fourier, soit le carré du nombre de pixels! Ce n’est pas rien et ce n’est en fait pas une opération réellement faisable en temps réel. Heureusement, en 1965, Cooley, Watson et Tukey ont trouvé une méthode pour réduire drastiquement le nombre de calculs à faire. Passant d’un million de millions d’opérations à seulement une dizaine de million (soit pratiquement un million fois moins d’opérations). Leur algorithme, que l’on appelle la transformée de Fourier rapide est réellement ce qui a démocratisé la transformée de Fourier. C’est l’un des algorithmes de traitement du signal le plus rapide qui existe.

Leur méthode de calcul utilise deux principes assez simples (en théorie, du moins parce qu’implémenter ce type d’algorithme est assez complexe). Le premier est la factorisation, il consiste à se rendre compte que pour calculer

3×2+3×4

Il faut 3 opérations (deux multiplications et une addition). Alors qu’en factorisant,

3x(2+4)

Il n’en faut plus que deux soit 30% d’amélioration! Sur aussi peu d’opérations, ce n’est pas grand-chose, mais sur un million de calculs, cela fait un vrai bol d’air! L’autre principe est que le nombre calcul de la transformée de Fourier est moins important si l’on subdivise le signal d’étude. Ainsi, s’il faut 256 opérations pour faire le calcul sur une image de 16 pixels (16×16 opérations), il en suffit de 128 si l’on prend le temps de couper l’image en deux (8×8+8×8 opérations). En répétant ainsi les subdivisions, le nombre d’étapes fond! Le plus intéressant dans leurs méthodes est qu’elle reste utilisable pour un grand nombre de dictionnaires et a donc permis de grandement accélérer les algorithmes de traitement du signal.

Le plus amusant là-dedans, c’est qu’on se soit demandé comment faire moins de calculs quand les machines ont remplacé les humains pour les faire… Entre le résultat de la transformée de Fourier tel que Fourier l’a définie, la généralisation donnée en l’imaginant comme une projection et le calcul rapide connu dans les années 70, la transformée de Fourier est aujourd’hui l’un des résultats mathématiques le plus utilisés!

 

Pour aller plus loin : 

•  God created the integers de Stephen Hawking : Un recueil de grands textes scientifiques avec à chaque fois une introduction sur les scientifiques concernés. Les textes scientifiques sont réservés aux spécialistes, mais les introductions sont accessibles et passionnantes! C’est dans ce livre que j’ai découvert que Fourier avait participé à l’expédition qui a permis la découverte de la pierre de Rosette
• Les mathématiciens aux éditions Pour la science : Plein d’éléments sur des grands mathématiciens. Le texte sur Fourier explique de manière très claire la transformée de Fourier rapide

Cet article est une reproduction du dossier que j’ai écrit pour Podcastscience et je vous engage à vous abonner à ce podcast. Pour les plus flemmards, le texte et l’audio dans la...