Cet article est une reproduction du dossier que j’ai écrit pour Podcastscience et je vous engage à vous abonner à ce podcast. Pour les plus flemmards, le texte et l’audio dans la suite…
L’infini est depuis toujours dans la tête des hommes sans pour autant qu’ils arrivent à l’appréhender. Parfois objet de fantasme, on le croise dans beaucoup de publicités allant des forfaits téléphoniques illimités aux restaurants à volonté. D’autres fois objet d’inquiétude devant son immensité comme a eu l’occasion de le dire Pascal :
Le silence éternel de ces espaces infinis me terrifie – Pascal
L’infini peut être très grand, mais aussi très petit. Dans l’antiquité, Zénon d’Élée présente une première approche de cet infiniment petit par le biais d’un paradoxe. Prenons deux points A et B représentés sur la figure ci-dessous.

Ce paradoxe explique qu’un objet ne peut aller de A à B en un temps fini. En effet, pour atteindre B en partant de A, cet objet doit passer par le milieu M du segment. Puis il doit passer par le milieu M’ de MB, puis par le milieu M” de M’B et ainsi de suite… L’objet doit donc passer par une infinité de points, ce qui est impossible (selon Zenon) en un temps fini.
Ce très vieux paradoxe illustre que l’on peut aussi croiser l’infini dans des espaces finis (ici le segment AB) en pratiquant une simple opération de découpage par deux. Pour plus de détails sur ce paradoxe et sa résolution, je vous invite à aller écouter le petit dossier de Mathieu sur le sujet dans le n°9 du podcast.
Chez les mathématiciens, l’infini a été un des plus importants sujets de discorde de l’histoire. Il y a un siècle seulement a eu lieu un véritable tremblement de terre au sein de la communauté mathématique au point que certains ont voulu éliminer l’infini des limites autorisées dans cette science! Tout cela à cause des travaux d’un seul homme, Georg Cantor, qui pour la première fois dans l’histoire réussissait à appréhender l’infini avec rigueur, mais certains de ses résultats remirent en cause les bases sur lesquelles se fondaient les mathématiques depuis des siècles.
Ce dossier présente les principaux résultats de ce “corrupteur de jeunesse” (c’est le nom que lui donnait un autre scientifique célèbre de l’époque, Kronecker) et quelques-unes de leurs implications.
Réapprendre à compter
Une des premières rencontres avec l’infini se fait très tôt, en répondant à la question “jusqu’à quel nombre sais-tu compter?”. Contrairement à l’affirmation commune, on n’arrive jamais à compter jusqu’à l’infini, mais on connait une méthode pour à partir d’un nombre donner, trouver le chiffre suivant. Roman Opalka, un artiste contemporain, a bien essayé de compter jusqu’à l’infini (une de ses peintures ci dessous), mais après 40 ans de travail, il trouve toujours le chiffre suivant!
Il n’est donc pas possible en temps fini de compter tous les nombres. Mais est-il possible de savoir s’il y a plus de nombres entiers :

que de nombres pairs :

La réponse semble être évidemment qu’il y a plus de nombres entiers que de nombres pairs étant donné que les nombres pairs sont strictement inclus dans les nombres, mais comment en être sûr?
Toutes les personnes ayant invité le temps d’une soirée des amis ont déjà trouvé, sans s’en rendre compte, une solution pour comparer efficacement des ensembles, même infinis! Pour qu’une soirée soit réussie, il est préférable que chaque invité ait un verre. On peut, bien sûr, compter le nombre des verres et le comparer avec le décompte du nombre d’invités. Étrangement, cette solution est rarement la plus efficace, que ce soit à cause d’un ami enfermé aux toilettes ou d’une erreur de compte pour cause d’ébriété.
Une méthode autrement plus efficace est de donner un verre à chaque invité. Si alors il reste des verres, c’est qu’il y a plus de verres que d’invité et inversement si des invités n’ont pas de verre c’est qu’il y a moins de verre que d’invité.
Pour comparer “l’ensemble des verres” et “l’ensemble des invités”, on a ainsi essayé d’associer à chaque invité un verre. Inversement, on sait retrouver à quel invité appartient le verre en regardant qui est au bout du bras qui le tient. Ce type d’application s’appelle en mathématique une “bijection”. Une bijection est une application entre deux espaces, elle associe à chaque élément de l’espace de départ (ici un invité) un unique élément de l’espace d’arrivée (ici un verre) et inversement à chaque élément de l’espace d’arrivée est associé un unique élément de l’espace de départ.
L’intérêt de ce type de transformation est de pouvoir comparer des ensembles. Ainsi, si chaque invité à un verre, on pourra dire que l’ensemble des verres contient autant d’éléments que l’ensemble des invités.
Armés de cette “bijection”, nous sommes à même de comparer des ensembles qu’ils soient finis ou infinis. Et c’est grâce à ce simple outil que Cantor a pu fabriquer sa théorie de l’infini.
Le merveilleux hôtel de Hilbert
Pour enseigner les nouvelles théories de Cantor, Hilbert, déjà un mathématicien célèbre à l’époque, propose une métaphore qui depuis porte son nom : l’Hôtel de Hilbert.
Cet hôtel est un lieu merveilleux puisqu’il contient une infinité de chambres. Et sa renommée à travers l’univers a fait ses preuves à tel point qu’aujourd’hui chacune des chambres est pleine. C’est-à-dire que quel que soit le numéro de chambre (par exemple la chambre n°1 345 765), il y a quelqu’un à l’intérieur. Un jour, se présente à la réception une personne souhaitant une chambre pour la nuit. Un propriétaire d’hôtel fini serait obligé de refuser cette nouvelle personne, mais le propriétaire de l’hôtel infini a plus d’un tour dans son sac. Il prend son micro et lance une annonce pour tous les résidents de l’hôtel :
“A chaque locataire, la direction a besoin de réorganiser l’hôtel, veuillez immédiatement rejoindre la chambre dont le numéro est immédiatement supérieur au vôtre. En nous excusant du dérangement”.
Ainsi, le locataire de la chambre 1 est maintenant dans la chambre 2
celui de la chambre 2 est maintenant dans la chambre 3
celui de la chambre 3 est maintenant dans la chambre 4
…
celui de la chambre 1 345 765 est maintenant dans la chambre 1 345 766
…
et ainsi de suite. Étant donné que chaque entier a un entier qui lui est directement supérieur, tous les locataires ont une chambre! Plus étonnant encore, grâce à cette réorganisation, il y a maintenant une place disponible dans la première chambre, on a donc
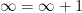
“Le tout est toujours plus grand que n’importe laquelle de ses parties”
Ici “le tout” est l’ensemble des entiers naturel, noté

et “une de ses partie” est l’ensemble des entiers plus grand ou égal à 2 :

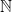
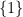
L’ensemble
…
…
Cette application associe bien à chaque entier de
Revenons-en à l’hôtel infini. Devant ce succès pour loger le nouvel arrivant, par le bouche à oreilles, le mois suivant un bus infini arrive à l’hôtel encore une fois complet! Gardant son flegme légendaire, le propriétaire lance l’annonce suivante :
“A chaque locataire, la direction a besoin de réorganiser l’hôtel, veuillez immédiatement rejoindre la chambre dont le numéro correspond au double de votre numéro de chambre actuel. En nous excusant du dérangement”.
Ainsi, le locataire de la chambre 1 est maintenant dans la chambre 2
celui de la chambre 2 est maintenant dans la chambre 4
celui de la chambre 3 est maintenant dans la chambre 6
…
celui de la chambre 1 345 765 est maintenant dans la chambre 2 691 530 (celui-ci aura un peu plus de marche que les autres).
…
et ainsi de suite.
Le propriétaire a ainsi libéré toutes les chambres ayant un numéro impair
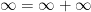
Ce résultat est correct, mais il est normal de ne pas l’accepter tout de suite, il va à l’encontre de l’intuition. Pourtant il est fondé, contrairement à l’intuition, sur un raisonnement logique. La vidéo ci-dessous résume avec brio ce qui vient d’être dit :
A ce stade, on a réussi à faire rentrer dans l’hôtel un ensemble infini qui paraissaient plus grand. On pourrait faire la même chose avec un bus infini qui possède une infinité d’étages, et ainsi de suite avec plusieurs ensembles infinis. En fait, les ensembles infinis “qui rentrent dans l’hôtel” ou, en termes plus mathématiques, les ensemble infinis pour lesquels il existe une bijection avec l’ensemble des entiers
Une fois l’infini dénombrable identifié et défini, il en suit automatiquement une autre question : existe-t-il d’autres types d’infinis? C’est la réponse à cette question qui constitue le résultat le plus connu de Cantor.
La bibliothèque de Babel
“La bibliothèque de Babel” est une nouvelle de Jorge Luis Borges. L’auteur y présente une bibliothèque dont l’une des caractéristiques est de contenir tous les livres pouvant exister. Plaçons-nous dans une telle bibliothèque et étendons les limites proposées par Borges (il ne considérait que des livres avec un nombre fini de pages). Imaginons que cette bibliothèque contient une infinité de livres qui chacun contiennent une infinité de pages. Comme Borges l’imagine, supposons alors que cette bibliothèque contient tous les textes possibles qu’ils soient lisibles ou non.
C’est-à-dire que quelque soit la suite (infini) de lettres ou “phrase” choisie :
on pourra trouver un livre de la bibliothèque qui lui correspond. Avec les exemples de l’hôtel de la partie précédente, on sait que l’on peut dénombrer les livres de la bibliothèque. On peut donc numéroter chacune des phrases infinies contenues dans chacun des livres de la bibliothèque :
Construisons alors la phrase constituée de la première lettre du premier livre 1, la deuxième du livre 2, la troisième du livre 3 et ainsi de suite (en gras ci dessous)…
On obtient la phrase qui commence par “auvoj…”. Maintenant, choisissons pour chaque lettre de cette phrase la suivante dans l’alphabet (si la lettre est un “z”, on choisira un “a”). La phrase obtenue commençant par “bvwpk…” ne peut pas être dans le livre 1, car la première lettre ne correspond pas, ne peut pas être dans le livre 2, car la deuxième lettre ne correspond pas, ne peut pas être dans le livre 3, car la troisième lettre ne correspond pas, etc. Cette phrase n’est dans aucun livre que contient la bibliothèque!
La seule hypothèse que nous avons pourtant faite est que la bibliothèque de Babel contient toutes les phrases possibles, c’est donc cette hypothèse qui est fausse. L’ensemble de toutes les phrases possible est un infini plus grand encore que l’infini dénombrable de l’ensemble des livres de la bibliothèque de Babel.
L’argument de la diagonale utilisé ici a été trouvé par Cantor en 1874. Pour la première fois, on distinguait deux infinis, l’infini dénombrable et l’infini indénombrable.
- L’infini dénombrable est celui de l’ensemble des entiers
- L’infini dit “continu” est celui de l’ensemble de toutes les phrases que l’on peut former ou encore celui de l’ensemble des nombres décimaux entre 0 et 1 ou encore l’ensemble des réels (c’est à dire l’ensemble des nombres décimaux avec une infinité de décimales).

On peut même amener l’ensemble des décimaux entre 0 et 1 (un segment) sur les réels (la droite). On va montrer ici comment associer les décimaux entre 0 et 1 sur la demi-droite positive. Une manière de faire est d’associer à chaque nombre x de
Cantor ne s’est pas arrêté là, il a montré qu’il existe d’autres infinis plus grands. En fait, il a donné une méthode pour, à partir d’un espace, construire un autre espace plus grand (n’étant pas en bijection). Cela permet de montrer qu’il y a en fait une infinité d’ensembles infinis plus grands les uns que les autres.
Sa méthode consiste à considérer “l’ensemble des parties” d’un ensemble. Prenons un exemple, l’ensemble qui contient les trois premiers entiers non nuls,

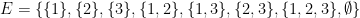
- Les ensembles ne contenant qu’un seul élément comme
- Les ensembles contenant deux éléments comme
- Les ensembles contenant trois éléments soit E
- L’ensemble vide noté
De l’ensemble à trois éléments E, on passe donc à huit éléments pour l’”ensemble des parties de E”. On peut en fait démonter que si un ensemble fini contient
Cantor a démontré que cela se généralise aux ensembles de taille infinie. Ce résultat a même pris son nom, c’est le Théorème de Cantor. Sa démonstration n’est encore une fois pas compliquée à comprendre mais un peu plus à accepter.
Etant un peu plus technique, je laisse les plus courageux cliquer ici pour dérouler cette démonstration.
Pour démontrer que l’ensemble des parties de E, que nous noterons maintenant P(E) ne peut pas être mis en bijection avec E, on va encore une fois raisonner par l’absurde en supposant que cela est possible.
Si ces deux ensembles peuvent être mis en bijection, alors il existe une bijection b qui à chaque élément de E associe un élément de P(E). C’est à dire, en gardant l’image de l’équipe de foot, qui à chaque individus associe un groupe de membres de l’équipe. Il peut alors se passer deux choses pour un membre de l’équipe donné :
- soit il fait parti du groupe qui lui est associé par la bijection
- soit il ne fait pas parti du groupe qui lui est associé par la bijection
Cantor propose alors de définir l’ensemble D des personnes qui ne sont pas dans le groupe qui leur est associé par la bijection. Mathématiquement, on le noterai
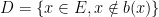

- Soit y est dans D, alors y n’appartient pas à
- Soit y n’est pas dans D, alors par définition y appartient à
D’où la contradiction! Très proche d’un paradoxe présenté par Russel, cette démonstration n’est pas des plus simples à accepter.
Le résultat du théorème de Cantor donne donc une méthode pour construire à partir d’un ensemble E un ensemble strictement plus grand P(E) et prouve donc qu’il existe une infinité d”infinis!
Ces démonstrations sur les infinis vont à l’encontre de l’intuition, mais sont parfaitement logiques. Les mathématiciens de l’époque ont été très perturbés et certains ont même cherché à bannir l’infini des mathématiques, mais la démonstration était là et était rigoureuse. Cantor lui-même, venant de démontrer un résultat similaire envoie un courrier célèbre à Dedekind, un de ses collègues avec qui il partageait ses résultats :
Tant que vous ne m’aurez pas approuvé, je ne puis que dire : je le vois, mais je ne le crois pas.
en d’autres termes, sa démonstration a prouvé le résultat, mais son esprit ne l’accepte pas encore.
Le problème irrésolu de Cantor
Après avoir montré que l’infini des réels était plus grand que l’infini des entiers, Cantor s’est demandé s’il existait des espaces entre ces deux infinis : avec strictement plus d’éléments que l’ensemble des entiers, mais moins que l’ensemble des réels. Il était convaincu qu’il n’existait aucun espace entre les entiers et les réels, cette hypothèse s’appelle “l’hypothèse du continu”. La démonstration de cette hypothèse l’occupa jusqu’à la fin de sa vie et ce n’est que 20 années après sa mort que tomba le résultat, l’hypothèse du continu est “indécidable”.
Une proposition indécidable (ou indépendante) est une proposition dont on ne peut ni montrer qu’elle est vraie ni montrer qu’elle est fausse. L’exemple le plus célèbre de proposition indécidable est l’axiome des parallèles d’Euclide :
Par un point extérieur à une droite, on ne peut tracer qu’une seule droite parallèle
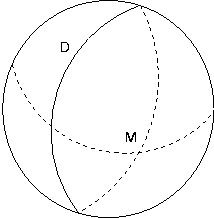
Dans son livre “Les Elements”, Euclide pose les bases de sa géométrie, les axiomes. Les axiomes sont des hypothèses admises du type “tous les angles droits sont égaux” ou encore “entre deux points on peut toujours tracer un segment”. Le 12e axiome d’Euclide, énoncé ci-dessus, paraît beaucoup plus complexe que les autres. Beaucoup de mathématiciens se sont donc demandé si on ne pouvait pas le démontrer grâce aux onze autres. Il a été montré qu’il était indécidable et on peut l’illustrer en présentant un exemple où cet axiome est faux (alors que les 11 autres restent vrais).
Sur une sphère (la terre par exemple), les “droites” sont les cercles qui ont pour diamètre le diamètre de la sphère. Sur le dessin ci dessous (trouvé sur Wikipedia) par exemple M et D sont deux “droites”
Deux droites parallèles sont définies par Euclide comme deux droites qui ne s’interserctent jamais. Sur la sphère pour un point extérieur à une droite il n’existe aucune droite parallèle. Toutes les droites étant des grands cercles (du diamètre de la sphère), elles s’intersectent nécessairement en au moins deux points. Cantor avait passé la fin de sa vie à essayer de démontrer une proposition qu’on ne pouvait démontrer.
Pour en savoir plus :
– CANTOR de Jean-Pierre Belna : Livre dont je me suis beaucoup servi, mais dont je déconseille la lecture à quelqu’un qui n’a pas l’habitude de lire des mathématiques, il n’est pas très pédagogique.
– Gödel Escher et Bach de hofstadter : Un livre immense, mais passionnant et accessible pour tout le monde. Il contient un petit passage sur la diagonale de Cantor
– The Infinite Book de hofstadter : en anglais, mais très accessible et très intéressant si le sujet de l’infini vous intéresse.
– Gödel de Pierre Cassou-Noguès : c’est dans ce livre où j’ai trouvé l’idée d’utiliser la bibliothèque de Babel pour montrer que l’infini continu et dénombrable n’avaient pas la même taille.
– Siv Books of Euclid de Byrne aux éditions Taschen : Le livre d’Euclide où il définit les éléments et présente les axiomes nécessaires à sa géométrie. La particularité de cette édition est d’avoir remplacé toutes les variables par des couleurs. Ceci simplifie la lecture et en fait un très bel objet.
– La villa des hommes de Denis Guedj : Je ne l’ai pas encore lu, mais il m’a été conseillé. C’est une fiction très largement inspirée de la vie de Cantor.


Laisser un commentaire