Cet article est une reproduction du dossier que j’ai écrit pour Podcastscience et je vous engage à vous abonner à ce podcast. Pour les plus flemmards, le texte et l’audio dans la suite…

[audio:http://www.podcastscience.fm/wp-content/uploads/2012/04/82-Les-algorithmes.mp3]

Pour un troisième dossier, on s’attaque aujourd’hui à un sujet très vaste, sans aucun doute le plus vieux de l’histoire des sciences… Lors du dossier sur Pi, nous avions pu découvrir que dès que l’homme a su écrire, il a parlé de la constante célèbre. Force est de constater que depuis que l’homme existe, il existe des algorithmes même si ce n’est que très récemment (au début du XX^e siècle) qu’une définition formelle à commencé à se montrer. Je serais même tenté d’affirmer que certains animaux usent d’algorithmes, mais devant ma méconnaissance du sujet, je laisserai des personnes plus compétentes apporter leur contribution une fois le dossier assimilé!

Un algorithme? Mais koikeskecédonc?

Depuis que l’homme existe donc et encore aujourd’hui, tout le monde utilise tous les jours, toutes les heures des algorithmes… Pour autant peu de personnes connaissent le mot et moins encore la définition exacte et cela est bien compréhensible tant elle est finalement complexe! Pourtant, l’idée est assez simple, voire même naturelle : une méthode qui, à partir de plusieurs données permet d’obtenir un résultat. Si cette définition n’est pas suffisamment précise pour bâtir une théorie mathématique, elle est suffisante pour donner à ce stade quelques exemples.

Commençons donc par le plus célèbre des algorithmes, celui que l’on a tous utilisé au moins une fois, celui qui est aussi vieux que l’invention du feu (ou presque) : la recette de cuisine! Dans toute bonne recette, à l’image de celle ci-dessous (provenant de l’excellent blog la foodbox), on a exactement les mêmes éléments…

Le nom nous permet de savoir à quoi sert cette recette, la liste d’ingrédients assure que l’on ait tous les outils et éléments nécessaires à sa réalisation. La procédure à suivre permet à n’importe qui, cuisinier ou non, intelligent ou non, de produire cette réalisation complexe. Les variantes et autres tests permettent de s’adapter à la situation et à l’envie.

Cet exemple traduit très bien l’idée partagée par nombre de scientifiques de la notion d’algorithme après l’apparition de ce mot au IX^e siècle. L’origine du mot algorithme est arabe, il correspond à la traduction du nom du mathématicien Al-Khwārizmī qui a accessoirement écrit un ouvrage qui a permis de propager en Europe l’écriture décimale positionnelle des nombres inventée par les Indiens (c’est celle que nous utilisons encore aujourd’hui). S’il n’y a pas aujourd’hui de définition simple communément acceptée de la notion d’algorithme, on y retrouve toujours les idées suivantes :

• Le dictionnaire de symboles, de mots est limité. Il se veut aussi simple et précis que possible. Dans le cas de la recette, ce dictionnaire de symboles est l’alphabet occidental accompagné de la ponctuation et des chiffres;
• On doit obtenir le résultat en un nombre fini d’étapes;
• Il doit pouvoir être suivi par un humain en ne nécessitant aucune intelligence, tout au plus, la capacité d’exécuter les différentes instructions. Cet aspect est particulièrement important pour les recettes. Si elles sont largement diffusées et utilisées, c’est entre autres parce qu’elles permettent d’obtenir un résultat proche du restaurant sans aucune connaissance préalable de cuisine.

À partir d’une définition aussi générale, vous comprendrez pourquoi j’affirme sans peur que c’est le plus vieux sujet scientifique : partout où il y a routine, méthode, transmission d’un savoir-faire, il y a algorithme! On pourrait donc pousser le vice jusqu’à considérer que les méthodes de chasse de nos ancêtres préhistoriques, qu’ils inscrivaient selon certaines théories sur les murs des grottes, étaient bel et bien des algorithmes.

Quelques algorithmes au cours de l’histoire

Pour autant, ce n’est que beaucoup plus tard qu’est généralement placée la date des premiers algorithmes principalement parce qu’il fallut attendre l’apparition de l’écriture pour avoir des traces des méthodes employées et non seulement de leur résultat. Dans le dossier sur Pi, je vous avais présenté une des premières apparitions du nombre sur le papyrus de Rhind. Ce papyrus, qui date de -2000, contient aussi des traces d’un algorithme pour réduire plusieurs fractions au même dénominateur. De manière plus générale, toutes les méthodes pour calculer Pi sont des algorithmes et sont un bon exemple de la diversité du sujet.

Datant cette même période des débuts de l’écriture, entre -3500 et -1500 av. J.-C., on a retrouvé des tablettes babyloniennes indiquant comment calculer un inverse, effectuer une division, etc. Ces opérations peuvent paraître simples aujourd’hui, mais en tant qu’algorithmes, les méthodes devenaient applicables par n’importe qui (sans culture ni éducation nécessaire). Ces méthodes permettaient de faire facilement des multiplications, des règles de trois, etc. Pour l’anecdote, cette civilisation ne comptait pas en base 10 (avec 10 chiffres), mais en base 60, cela simplifie les divisions. Le choix de la base 60 s’explique probablement du nombre de phalanges des doigts d’une main (sans compter le pouce) et du nombre de doigts de la main (5×12=60). À titre d’anecdotes à ressortir en dîner de famille, c’est parce que les Babyloniens comptaient en base 60 que nous comptons 60 minutes dans une heure.

Il n’y a pas que ces vieilles civilisations qui s’aidaient d’algorithmes pour effectuer des opérations simples. Lorsque vous posez une division, vous effectuez des étapes mécaniques sans forcément savoir pourquoi elles fonctionnent, mais au contraire, vous avez appris par cœur un rituel qui permet de vite effectuer l’opération. Parmi les outils originaux pour effectuer des opérations simples, l’image ci-dessous (provenant de Wikipedia) représente l’invention de Lucas-Genaille : un système de réglettes pour effectuer la multiplication de deux grands nombres.

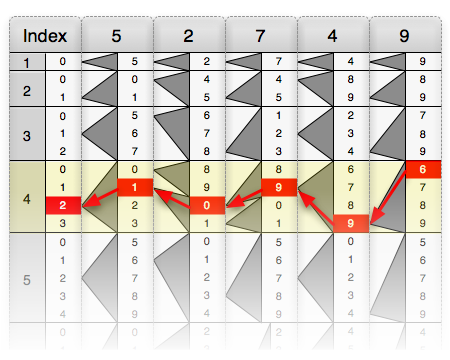
Pour effectuer la multiplication, il suffit de placer les réglettes correspondant au nombre choisi et de suivre les flèches noires comme sur la figure ci-dessous (provenant tout autant de Wikipedia).

Dans cet exemple, on effectue la multiplication de 52749 par 4 : en suivant les flèches noires, on trouve 210996. Ces réglettes furent commercialisées jusqu’en 1911! Ce système aussi amusant qu’ingénieux est une goutte d’eau au milieu des autres méthodes permettant de faire des opérations arithmétiques.

De tout temps, les algorithmes ont donc été au centre de l’activité humaine, mais il fallut attendre 1900 pour voir apparaître un début de formalisation de ce concept avec le 10^e problème de Hilbert, nous y revenons dans la prochaine partie. Il n’a pas fallu attendre la formalisation pour voir apparaître des algorithmes très complexes. Jusqu’à cette période, le mot algorithme était le plus souvent associé à Euclide et une manière simple de présenter la notion d’algorithme était de donner l’exemple du célèbre calcul.

Algorithme d’Euclide

Euclide écrit au troisième siècle  av. J.-C. 13 livres « les éléments« . Les premiers traitent de géométrie alors que les livres VII, VIII et IX posent les bases de la théorie des nombres. C’est justement dans le 7^e livre qu’Euclide présente une méthode pour calculer le plus grand diviseur commun à deux nombres. Le plus grand diviseur commun de a et b, PGCD pour les intimes, est le plus grand nombre qui divise a et b (c’est-à-dire le plus grand nombre p tel que a/p et b/p soient entiers). Nous ne reviendrons pas ici sur la preuve du fonctionnement de l’algorithme ni sur la théorie des nombres, car ce n’est pas le sujet.

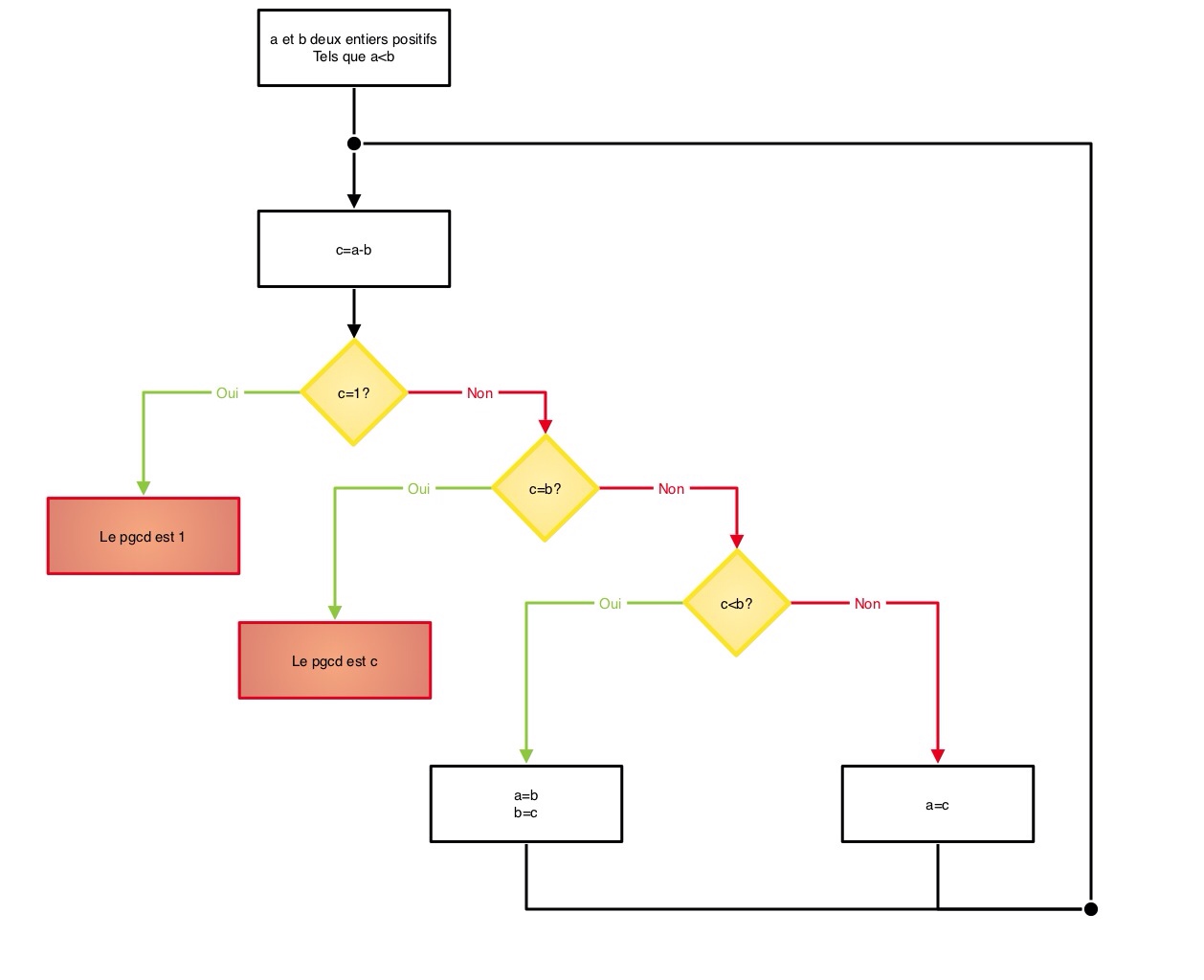
Bien qu’il soit très vieux, cet algorithme reste d’actualité et contient tous les éléments d’un algorithme « moderne ». Son fonctionnement tel que décrit dans le livre est résumé par la figure suivante. Pour les puristes, l’algorithme présenté ici est celui décrit par Euclide dans son livre et non l’amélioration utilisant la division euclidienne généralement présentée.

C’est un algorithme très utile et encore très utilisé, car il à été généralisé pour plusieurs résultats, par exemple, il permet de calculer les coefficients de l’identité de bezout qui sert dans le système de cryptage RSA, énormément utilisé pour la sécurisation du e-commerce. C’est l’un des plus vieux algorithmes encore en activité.

On y retrouve encore nombre d’éléments de la recette de cuisine :

• Des déclarations : trois variables sont déclarées (a, b et c) même si avec le seul schéma ci-dessus, cela est sous-entendu. Dans la recette, la liste d’ingrédients joue ce rôle de déclaration. En plus de cela, est comme c’est parfois précisé, il faudrait « déclarer » quels sont les ustensiles nécessaires.
• Des affectations : les trois variables se voient affecter plusieurs résultats tout au long de l’algorithme. Dans la recette, c’est le contenu des bols et autres assiettes qui joue ce rôle d’affectation.
• Une séquence d’instruction : les flèches sur le diagramme permettent de savoir dans quel ordre effectuer les opérations. Dans la recette, c’est l’ordre des phrases.
• Des tests : « c=1 » par exemple. Dans la recette, on trouvait le test « est-ce que le chou est croquant? »
• Une boucle : dans cet algorithme, la même opération est répétée jusqu’à ce que l’on trouve le PGCD. Dans la recette, on fait cuire le chou tant qu’il est « croquant » jusqu’à ce qu’il devienne « un peu croquant ».

Et surtout, l’algorithme d’Euclide correspond bien à l’idée de ce qu’est un algorithme présenté en début de dossier. Les souhaits présentés dans la première liste correspondent à ce que l’on attend d’un algorithme alors que cette nouvelle liste correspond à 5 outils qui permettent de construire des objets correspondant à la première intention. Deux questions s’imposent alors : ces 5 outils sont-ils indispensables? Et surtout est-ce qu’avec ces seuls 5 outils, on peut construire tous les algorithmes correspondants aux désirs énoncés? Avant de répondre à ces deux questions, nous allons faire un petit écart historique pour dire deux mots sur l’événement qui amena à une meilleure définition des algorithmes et déclencha les nombreux travaux qui aboutirent à leur réponse.

La fin du formalisme de Hilbert

En 1900, au congrès international des mathématiciens, Hilbert présenta 23 problèmes non résolus qui selon lui étaient les plus importants du moment. Un certain nombre sont aujourd’hui résolus : c’est-à-dire que l’on a montré qu’ils étaient soit vrais soit faux. Ou alors on a prouvé qu’ils étaient indécidables, qu’on ne peut pas dire s’ils sont vrais ou faux; ils sont indépendants de la théorie considérée. Un équivalent aujourd’hui de cette démarche est les problèmes du prix du millénaire pour lesquels l’institut mathématique Clay offre un million de dollars à qui apporte une solution (et pour information, cette somme ne serait qu’un pourboire tant la plupart de ces problèmes sont importants et ont plusieurs applications cruciales telles que la cryptographie).

Hilbert dans sa démarche visait à montrer une certaine « perfection » des mathématiques en demandant la démonstration de trois résultats :

• La complétude des mathématiques : c’est-à-dire que tout énoncé peut être confirmé ou infirmé. En d’autres termes que l’on peut construire une théorie sans aucune proposition indécidable;
• La consistance des mathématiques : c’est-à-dire qu’il n’existe pas d’énoncé contradictoire, qui serait vrai ainsi que son contraire;
• La décision des propositions mathématiques : c’est-à-dire qu’il existe une procédure s’exécutant en un temps fini permettant de démontrer qu’un énoncé mathématique est vrai.

Ironie de l’histoire, alors qu’Hilbert souhaitait que tous ces énoncés soient vrais, il fallut moins de 50 ans pour démontrer qu’il n’existait pas de théorie mathématique suffisamment complexe pour contenir les opérations élémentaires (addition, multiplication, inverse…) à la fois consistante et complète. Et surtout qu’une procédure qui permet de décider si un énoncé est vrai en un temps fini n’existe pas. Une défaite pour la pensée de Hilbert, mais grâce à ses problèmes, une avancée exceptionnelle des mathématiques et de la connaissance de leurs limites.

La dernière question, qui correspond au 10^e problème de Hilbert, parle sans s’en rendre compte d’algorithme. En effet, Hilbert souhaite trouver une méthode qui s’exécute en un nombre fini d’étapes pour obtenir son résultat. Et pour apporter une solution à ce problème (la solution est que c’est impossible, mais ça reste une solution), il fallut bien définir la notion d’algorithme. Et grâce à cette bonne définition, on put en cerner certaines limites.

La caractérisation précise des algorithmes a pu se faire en définissant la notion de fonction calculable, c’est-à-dire une fonction qui coïncide avec la description faite en début de dossier. Beaucoup de très grands noms des mathématiques du XX^e siècle ont proposé une définition de la calculabilité. Il y a d’abord Godel, qui après avoir détruit les rêves de Hilbert sur l’incomplétude et la cohérence présenta une définition de « fonctions récursives » conçues sur quelques règles simples. Alonzo Church démontra l’impossibilité du problème de décision posé par Hilbert, résultat qui a aujourd’hui son nom. Il créa de son côté le lambda calcul, qui tout comme les fonctions récursives de Godel, avait pour but de représenter les algorithmes. Enfin, Turing proposa encore une autre construction, les machines de Turing, dont nous allons reparler tout de suite.

Entre 1931 et 1936, divers scientifiques brillants ont proposé plusieurs définitions de fonctions calculables qui paraissaient toutes aussi pertinentes. En fait toutes ces constructions sont équivalentes, les algorithmes que l’on peut construire avec sont les mêmes! Il n’y avait donc en fait qu’un ensemble de fonctions, de méthodes que l’on pouvait fabriquer et c’est ce que l’on appelle aujourd’hui les algorithmes. Dans la partie suivante, nous allons voir l’une de ces constructions, sans aucun doute la plus célèbre : la machine de Turing.

Machine de Turing

Il n’a pas été facile de choisir la définition de fonction calculable que j’allais présenter pour ce dossier. À vrai dire, je ne savais pas qu’il y en avait autant et surtout celle des machines de Turing était de loin celle qui me parlait le moins, me paraissait la moins intuitive. Puis, j’ai lu l’extrait traduit de « on the computable numbers, with an application to the Entscheidungsproblem » que vous pourrez trouver dans « histoires d’algorithmes », livre dont la référence complète est donnée en fin de dossier. Si vous le pouvez, lisez le texte directement, c’est limpide et explique très simplement la construction de ces « machines ».

Turing cherche donc à formaliser l’opération que l’on appelle intuitivement « calcul ». Il commence par énumérer les différents éléments nécessaires pour faire un calcul. Le calcul est fait sur une feuille où l’on écrit les symboles les uns après les autres sur une ligne. Il propose donc de modéliser cela par un ruban de papier quadrillé. Il explique ensuite qu’on doit se limiter à un nombre fini de symboles tels que dans notre alphabet et précise que l’un de ces symboles doit être repéré comme étant le « 0 », la case vierge.

Tout comme nous ne regardons qu’une étape de recette à la fois, Turing poursuit en disant qu’un calculateur ne peut observer qu’un nombre de symboles fini fixé à chaque étape. Et tout comme le plat est dans un état bien déterminé et le cuisinier dans un état d’esprit bien précis avant le début d’une étape, il précise que sa machine est dans un nombre fini d’états au moment de l’observation.

Il explique ensuite que la donnée de l’état du calculateur et de l’observation des symboles permet d’effectuer deux opérations :

• changer l’ordre des cases en échangeant une case observée par une case voisine ;
• remplacer le symbole dans une case du ruban par un nouveau.

Lorsque l’on suit une recette de cuisine, on n’effectue pas autre chose, on ajoute et retire des ingrédients, on les mélange… Si l’on décompose la recette au maximum en opérations simples, on arrive à rester dans la modélisation de Turing.

Et… C’est tout! À partir de cette construction, on arrive à modéliser toutes les choses que nous appelons ou soupçonnons être à ce jour des « algorithmes ». En fait, ce que nous appelons aujourd’hui une machine de Turing est encore plus simple et permet de fabriquer exactement les mêmes systèmes : l’alphabet n’a que deux symboles (0 et 1), on observe une seule case à la fois et on ne peut utiliser que les cases directement voisines à la case observée.

Il fut montré que les machines de Turing sont équivalentes à toutes les autres fonctions « calculables » de l’époque et on ne connaît pas à ce jour de « méthode » exécutable par une machine, un humain ou un animal qui ne soit pas modélisable par l’une d’elles. Mais pour autant, est-ce que ces fonctions calculables correspondent bien à l’intuition de la notion d’algorithme? Alonzo Church en était convaincu et cette hypothèse est aujourd’hui connue sous le nom de « thèse de Church« . Autant dire tout de suite que cette conjecture à peu d’espoir d’être démontrée tant elle est plus proche de la philosophie que des sciences (allez donc jeter un oeil à la conférence mise en lien en fin de dossier si le sujet vous intéresse)… D’autant plus que grâce aux raisonnements de Cantor, on peut démontrer que l’ensemble des fonctions calculables est dénombrable. Comme l’ensemble des nombres réels est indénombrable, il existe une infinité de nombres non calculables par des algorithmes! Reste à savoir si ce sont des nombres atteignables dans le monde « réel ».

Savoir calculer ne suffit pas

Une fois la notion de fonction calculable posée et la thèse de Church avancées, nous savions que nous avions en main tous les outils pour créer des algorithmes des plus complexes. Pourtant, cela est encore trop théorique. Dans les faits, avec l’arrivée des ordinateurs, pourtant dotés d’une capacité de calcul énorme (tout en étant parfaitement stupides, ce qui colle bien avec la définition d’un algorithme), on s’est rendu compte qu’une autre limitation empêchait de finir certains calculs.

Dans le cher monde réel, dire que l’on obtiendra un résultat en un temps fini ne suffit pas, parce que cela n’empêche pas par exemple que le temps d’exécution d’un algorithme prenne plusieurs fois l’âge de l’univers pour s’exécuter (sisi, c’est très grand, mais c’est fini).  Dans le guide du voyageur galactique par exemple, des habitants d’une planète construisent une machine pour répondre à la grande question sur la vie l’univers et tout le reste et ce n’est que 7 millions et demi d’années plus tard que la réponse, 42, est obtenue!

La complexité algorithmique est l’objet de l’un des 7 problèmes à un million de dollars et déjà traité dans le tout premier épisode du podcast (contrairement à ce que l’on a cru brièvement a l’époque, le problème est toujours ouvert). Ce problème, que l’on résume souvent à « P=NP » est selon la plupart des mathématiciens à la fois le plus important de ceux de l’institut Clay et le plus à même à être résolu par un amateur. Certains problèmes appartiennent à la catégorie P (les plus « simples ») et d’autres a la catégorie NP (les plus complexes), tout l’enjeu du problème est de prouver que ces catégories sont les mêmes. Et pour le démontrer, il suffirait soit de prouver qu’un seul problème NP n’est pas P (on a alors P different de NP) ou qu’un seul problème NP-Complet (classe particulière de problèmes NP qui sont équivalents à tous les autres) est en fait dans P (alors P=NP), voilà pourquoi beaucoup pensent qu’un amateur pourrait apporter une solution.

Ce qui différencie ces problèmes, c’est la complexité des algorithmes que l’on connaît pour les résoudre. La complexité d’un algorithme est un ordre de grandeur du temps qu’il faut pour obtenir un résultat en fonction de la taille des données du problème dans le pire des cas. Prenons un exemple amusant qui a été posé à un ami lors d’un entretien d’embauche.

Imaginons que vous ayez une noix de coco et devant vous un immeuble de n étages. Vous souhaitez savoir à quel étage exactement la noix de coco se casse. La seule solution dans ce cas, et d’aller à chaque étage en commençant par le rez-de-chaussée et de lâcher la noix de coco pour voir si elle se casse (on suppose que la noix de coco ne s’abîme pas, soit elle se casse soit elle reste indemne). Dans le pire des cas, c’est au dernier étage que la noix de coco se casse, il faut donc faire n tests.

Avec deux noix de coco, le problème devient plus intéressant. Ce qui vient tout de suite à l’esprit est de balancer la première noix de coco à la moitié du bâtiment puis en fonction de la casse à la moitié de la moitié restante et ainsi de suite jusqu’à ce qu’elle casse et de finir avec l’autre en testant tous les étages restants.

Mais quitte à séparer le bâtiment en deux parties, on peut le séparer en 3, 4, 5 ou plus généralement k parties. Il faudra alors au pire des cas que l’on effectue k tests avec la première noix de coco puis n/k tests (les étages restants) avec la deuxième noix de coco. On effectue donc opérations. Il s’agit alors de trouver pour quel k on effectuera le moins d’opérations.

C’est à dire de trouver le nombre m tel que pour toutes les valeurs de k, soit supérieur à m. Autrement dit que est supérieur à zéro pour tous les k. Comme k est supérieur à zéro, cela revient à trouver le minimum du polynôme .

Pour résoudre un polynôme de degré 2, rappelez-vous de l’algorithme appris à l’école ou allez consulter votre mémoire numérique Wikipédia, il faut calculer le déterminant qui vaut pour le polynôme . Dans notre cas, il vaut donc :

Pour qu’un polynôme ne change pas de signe, il faut qu’il ait une racine double (le fameux cas rappelez vous!), c’est-à-dire que . Le k pour lequel est atteint ce minimum est alors . Il faut donc diviser le bâtiment en racine carrée du nombre d’étages pour aller au plus vite à la solution (on obtient alors le résultat en opérations).

Ces exemples montrent que l’on peut résoudre un même problème de façon plus ou moins rapide. Dans les cas présents, si l’on passe d’un bâtiment de 10 étages à un bâtiment qui en a 100 000, dans le premier cas, on multiplie le nombre d’opérations par 10000 alors que dans le second on le multiplie seulement par 100. Cela peut dans certains cas différencier un algorithme exécutable en temps humain d’un algorithme dont nous ne verrons jamais la fin.

Pour revenir au problème P=NP, les problèmes P sont ceux pour lesquelles ont connaît un algorithme qui ne nécessite « que » un nombre polynomial d’opérations par rapport à la taille des données d’entrée. C’est-à-dire que le nombre d’opérations qu’ils nécessitent pour des données de taille n est inférieur à pour un certain k. Les problèmes NP sont quant à eux des problèmes dont on ne connaît pas d’algorithme les résolvant en temps polynomial, mais où il est facile de vérifier si l’on a une solution (facile veut dire que cette vérification se fait en temps polynomial). Dans l’exemple de la noix de coco, même s’il faut n opérations pour résoudre le problème il n’en faut qu’une seule pour voir si la noix de coco est cassée.

Les problèmes NP sont alors des problèmes que l’on résout facilement avec de la chance : en prenant une configuration au hasard et pour peu qu’on soit par chance tombé sur la solution, on sait s’en rendre compte rapidement. Toute la question de P=NP est alors de savoir si des problèmes simples à vérifier sont simples à résoudre.

Les problèmes NP ne sont pas du tout des problèmes exotiques mis en avant par un mathématicien un peu fou, ce sont des problèmes que l’on croise tous les jours. Le plus connu, le voyageur de commerce, demande à proposer une méthode pour trouver le chemin le plus court étant donné une répartition de maisons pour que le voyageur de commerce puisse toutes les voir. On sait facilement vérifier si l’on a bien le chemin le plus court, mais on ne sait pas facilement trouver ce chemin.

Plus amusant, étant donné une liste de mots et un mot croisé vierge, trouver où il faut mettre chaque mot est un problème NP, on sait très rapidement vérifier si la grille est bien remplie, mais on ne sait pas la remplir rapidement.

Ce problème reste aujourd’hui complètement ouvert. À une époque, on pensait qu’il était vrai, aujourd’hui beaucoup pensent qu’il est faux et d’autres qu’il serait indécidable…..

Ici s’achève le dossier sur les algorithmes, j’espère vous avoir éclairé sur le sujet et surtout vous avoir démontré que l’on pouvait parler d’algorithmes sans jamais parler d’ordinateur ni de langage de programmation!

Sources bibliographiques et autres liens pour aller plus loin :

• « histoires d’algorithmes : du caillou a la puce » : un excellent livre qui regorge d’exemples d’algorithmes. On y trouve le texte original, sa traduction quand c’est nécessaire et des explications historiques, c’est de loin celui qui m’al le plus servi a construire ce dossier.
• « Godel Escher et Bach : Les Brins d’une Guirlande Eternelle » : un livre référence en diffusion des mathématiques qui traite sur une grande part de ce sujet. Contrairement au précédent qui a une approche très historique, celui-ci a une approche plus poétique et plus imagée tout en restant parfaitement rigoureux.
• « les métamorphoses du calcul : une étonnante histoire des mathématiques » : un livre qui parle de Math et qui a eu le prix de philosophie de l’académie française! Livre qui parle de l’histoire du calcul et de la thèse de Church, ses implications, de la philosophie autour de cette hypothèse. Ce livre est écrit par un très bon pédagogue et est passionnant, pour autant, il ne faut pas oublier à la lecture que c’est le livre d’un informaticien, parfois un peu trop convaincu de la supériorité du calcul sur les mathématiques au sens large (calculables ou non).
• Gilles Dowek qui a écrit le livre précédent est écoutable et visionable dans une conférence. Elle nécessite l’instalation de l’horreur « Real Player » mais je vous assure que cela vaut le coup!
• « Dossier pour la science : Les grands problèmes mathématiques » : un excellent numéro sur les problèmes a un million de dollars et sur quelques uns des problèmes de Hilbert.
• « on the computable numbers, with an application to the Entscheidungsproblem » Le papier original de Turing en anglais
• La recette a base de choux fractal : je ne suis pas responsable de la qualité de la recette, je ne l’ai pas testé!

merci à Sébastien pour le problème des noix de coco.

Cet article est une reproduction du dossier que j’ai écrit pour Podcastscience et je vous engage à vous abonner à ce podcast. Pour les plus flemmards, le texte et l’audio...