Cet article est une reproduction du dossier que j’ai écrit pour Podcastscience et je vous engage à vous abonner à ce podcast. Pour les plus flemmards, le texte et l’audio dans la suite…

[audio:http://www.podcastscience.fm/wp-content/uploads/2012/03/77-Pi.mp3]

Si nous faisons aujourd’hui une émission sur pi, c’est avant tout parce que le 14 mars est une date très spéciale. Aux États-Unis, on note d’abord le mois puis le jour pour indiquer la date, nous sommes donc le 3-14, ce qui correspond à une estimation des premières décimales de ! Cette journée festive pour les mathématiciens est l’occasion de manger des pie (tartes) en buvant des piña colada. Pour l’anecdote, c’est le jour où le MIT dévoile ses admissions, il le fait à 1:59pm (les décimales suivantes dans pi)

Plusieurs nombres ont un statut particulier en mathématiques, principalement du fait de leur histoire. Les plus célèbres sont sans aucun doute , le nombre d’or, exponentielle, et oméga (celui-là, vous ne le connaissez probablement pas, j’en parle un peu plus loin dans ce dossier). Cette illustration d’XKCD résume assez bien l’ensemble des nombres “intéressants” pour les mathématiens.

garde un statut particulier, c’est avec celui dont la définition est la plus simple et pourtant il a, du fait de ses propriétés complexes perturbées de nombreux scientifiques de l’histoire. Dans ce dossier, nous verrons quelques-unes des propriétés de ce nombre unique.

Je ne vais pas m’attarder trop longtemps sur la définition la plus connue de , à savoir le rapport entre la circonférence (longueur du périmètre d’un cercle) et son diamètre. Ni de la définition qui suit généralement à savoir le rapport entre l’aire du cercle et le carré de son rayon. En revanche, nous allons commencer par répondre à une question que vous ne vous êtes sans doute pas assez posée est-il constant?

Pi est-il constant?

La réponse largement acceptée à cette question est oui. Pourtant cela reste à démontrer. Une démonstration simple utilise un théorème que l’on voit à l’école : le théorème de Thalès. Son énoncé est le suivant :
“Soit un triangle ABC et deux points D et E tels que les droites (DE) et (BC) soient parallèles. Alors on a ”
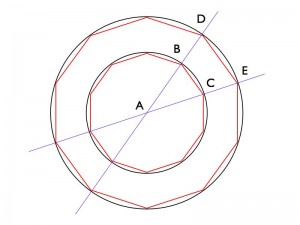
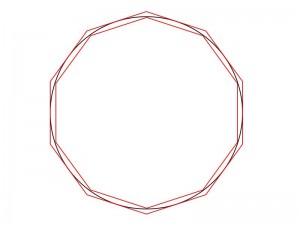
Si l’on prend alors deux cercles de rayon différents et que l’on trace le plus grand polygone de 10 côtés à l’intérieur, on obtient la figure suivante :

Le théorème de Thalès permet d’affirmer que le rapport entre les côtés de chaque polygones sont égaux au rapport des rayons des deux cercles :

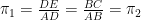
Si on augmente le nombre de côtés des deux polygones, les “rayons” des polygones convergent vers la même valeur et le rapport des circonférences est donc égal au rapport des rayons, les des deux cercles sont donc égaux (pour que la démonstration soit juste, il ne faut pas se contenter de tracer le plus grand polygone contenu dans le cercle, mais tracer aussi le plus petit qui contient le cercle).

Ouf, est constant, on ne nous a pas menti! Enfin, comme toute démonstration mathématique, elle est vraie dans le cadre de certaines hypothèses… Pour que le théorème de Thalès soit vrai, il faut se placer dans la géométrie d’Euclide, soit grossièrement une géométrie “plate” en opposition à une géométrie courbe. Prenons par exemple une assiette à soupe. Le pourtour de l’assiette forme bien un cercle, mais le centre de ce cercle, sur l’assiette, n’est pas sur le même plan que ce cercle et ne coïncide donc pas avec le centre « euclidien » du cercle. Sur Terre, le problème est le même, du fait de la forme de la terre, quand on trace un cercle au sol et mesure son diamètre, la valeur n’est pas la même que celle que l’on obtiendrait en géométrie euclidienne. Cela a pour conséquence que sur Terre n’est pas constant!

Rassurez-vous, le des mathématiques est bel est bien constant et correspond au rapport des cercles en géométrie Euclicienne. Cette remarque permet de différencier deux types de constantes :

•  Les constantes “physiques” : Des expériences laissent penser qu’une opération donne toujours le même résultat quelles que soient un certain nombre de transformations subies par un objet (par exemple en traçant plusieurs cercles sur le sol et en mesurant diamètre et circonférence, on constate que le rapport fait toujours la même valeur).
• Les constantes “mathématiques” : Grâce à plusieurs hypothèses, on a démontré que cette valeur était constante.

Dans l’histoire, a d’abord été une constante physique, il n’est devenu constante mathématique assez tard grâce à l’homme dont l’un des bains est le plus célèbre de l’histoire.

Les premières apparitions

Une des premières apparitions de , ou du moins de l’idée d’un rapport constant entre la circonférence du cercle et de son rayon, provient d’une tablette babylonienne datant d’environ 2000 avjc. Grâce à l’hexagone inscrit dans un cercle, les Babyloniens avaient proposé l’approximation .
Les Égyptiens quant à eux ont laissé la trace d’un calcul implicite de sur le papyrus de Rhind. Ce papyrus, rédigé par le scribe Ahmès environ 1650 ans avant notre ère, est la recopie d’un manuel scolaire un peu plus vieux (1800 avjc environ) et est représenté sur l’image ci-dessous (trouvée sur wikipedia).

Sur ce papyrus, on donne une méthode pour calculer la surface d’un cercle à partir de son diamètre D :

• Enlever 1/9 au diamètre du cercle
• multiplier le résultat par lui-même

Soit la formule au lieu de soit une estimation de pi à .
Notons que rien ne prouve aujourd’hui que les Babyloniens ou les Égyptiens savaient si leurs valeurs de était exacte ou une approximation. Ils avaient expérimentalement constaté qu’il existait un rapport constant et l’avaient estimé par diverses manières.

Et pi devint mathématique

Ce n’est que beaucoup plus tard, autour de 250 avjc qu’Archimède transforme la constante physique en une constante mathématique. Dans le traité “De la mesure du cercle”, il calcule des encadrements de . Pour calculer ces encadrements, il utilise des polygones réguliers (un polygone régulier à n côtés est une figure ayant n côtés égaux). Pour encadrer la circonférence d’un cercle, il encadre le dit cercle par le plus petit polygone qui contient le cercle et le plus grand polygone contenu dans le cercle (comme dans la figure ci-dessous).

Ce type de construction permet non seulement de calculer à la précision que l’on souhaite (en prenant des polygones avec de plus en plus de côtés), mais permet aussi de démontrer que est bien une constante mathématique.

Pourquoi faire simple quand on peut faire compliqué?

Il existe de nombreuses autres manières pour définir . Un constat simple est que partout où l’on trouve un cercle ou une sphère, on peut trouver . Ainsi, le volume d’une sphère dépendra de (), sa surface aussi () ainsi que la probabilité pour un cure-dent que vous lancez sur votre parquet de croiser un rainure (l’ensemble des sens selon lequel le cure-dent tombe sur le sol forme un cercle). Aujourd’hui, ces définitions géométriques sont très peu utilisées, les mathématiciens y préfèrent des définitions plus abstraites, mais aussi plus faciles à manipuler.

On peut par exemple définir en disant que c’est l’unique nombre x tel que cos(x)=0. Ayant bien sûr avant défini cosinus grâce à des exponentielles complexes et l’exponentielle grâce à une somme infinie de termes, ayant alors posé la théorie des sommes infinies et des nombres complexes… Autant dire que l’on est loin de la simplicité géométrique. Pourtant, ce type de définition permet de démontrer des résultats très élégants et pratiques pour calculer :

A l’école, les plus jeunes auront appris que vaut à peu près 3,14 et les plus vieux 22/7, ces deux nombres très simples sont hélas des approximations. On a d’un côté une définition très simple de et de l’autre des formules très compliquées (une infinité de termes) pour le calculer, n’y a-t-il pas une formule plus simple? Durant toute l’histoire, les mathématiciens ont essayé de ranger dans des ensembles de nombres qui par leur propriétés simplifieraient le calcul, sans succès. Ils ont ainsi rendu célèbre pour tout ce qu’il est pas!

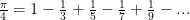
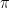
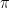
Ce que pi n’est pas!

Les premier nombres qui furent utilisés sont les nombres dit “naturels” :

L’ensemble de tous ces nombres est noté . Assez rapidement le besoin s’est fait sentir d’avoir des nombres négatifs. Les nombres négatifs sont les inverses pour l’addition des entiers naturels. C’est à dire qu’en additionnant un entier naturel, 3 par exemple, et son inverse, -3 dans ce cas, on obtient 0. Cet ensemble, bien que simple permet, avec les opérations que l’on connaît tous d’addition “+” et de multiplication “x” (on rappellera que la soustraction n’est pas une “vraie” opération, c’est l’addition de l’opposé), offre déjà la possibilité de faire les opérations d’arithmétique classique. C’est-à-dire que l’on peut y définir des polynômes ( par exemple), la division euclidienne (celle que l’on apprend à la petite école : la division de 13 par 4 a pour reste 1), etc.

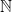
Malheureusement et pour revenir à notre sujet, on s’est très rapidement rendu compte que n’est pas un entier. En fait, je n’ai vu qu’un texte qui présentait comme un entier (ou plutôt une approximation, le texte en question datant de 500 avjc, on ne parle pas du moderne) : la Bible. On peut en effet y lire :

“Il fit aussi une mer de fonte de dix coudées d’un bord jusqu’à l’autre, qui était toute ronde : elle avait cinq coudées de haut et était environnée tout à l’entour d’un cordon de trente coudées”

Pi n’est pas aimé des Py-taghoriciens

Les entiers relatifs ne suffisent pas à décrire . En fait, ils ne suffisent pas non plus à décrire la plupart des nombres que nous utilisons chaque jour. Quand on mange un gâteau par exemple, on est très vite amenés à parler du tiers ou du quart du gâteau. On est très habitués à parler en “fractions”. Une fraction s’écrit comme le rapport de deux entiers relatifs (1/3, 2/5, 1242332/58974892676, etc.)

Les fractions sont très utiles pour représenter des quantités intrinsèquement non entières. Par exemple, 1/3 permet de séparer en trois l’unité. L’École Pythagoricienne, qui exista autour des années 500 avjc, était persuadée que tous les nombres pouvaient être représentés par des fractions. Cette école philosophique (qui serait sans doute qualifiée de secte si elle existait encore aujourd’hui) pensait que le rapport entre toute quantité du même type peut être rapporté au rapport entre deux entiers. L’ensemble des fractions paraissait alors si “normal” qu’il est appelé aujourd’hui ensemble des “Rationnels”.
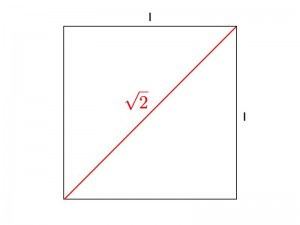
On ne sait sous quelles conditions, mais un jour les pythagoriciens sont tombés devant un paradoxe de taille. Si l’on trace un carré de côté 1, la diagonale de ce carré a pour longueur (le nombre qui multiplié par lui même fait 2).

Une ironie amusante est que l’on peut démontrer que cette diagonale correspond à grâce au théorème de Pythagore (La paternité du théorème qu’indique ce nom est très loin d’être certifiée…) Ce nombre dont le carré vaut 2 est-il rationnel, autrement dit, peut-on l’écrire sous forme de fraction?
Regardons cela de plus près. Dire que est rationnel revient à dire qu’il existe des entiers positifs p et q non nuls tels que

En élevant cette relation au carré et en multipliant par q, on obtient

Cette relation permet de déduire que est pair. Nous allons réécrire les nombres p et q afin de compter “le nombre de fois où ils sont pairs” :

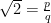
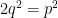
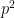
où r est impair.

On peut dire alors que p est pair j fois. Le carré de p se décompose alors :

n’est pas pair car le carré d’un nombre impair est impair. On peut donc affirmer que le nombre de fois où est pair est 2j.

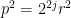
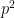
Effectuons le même raisonnement sur q en notant k le nombre de fois où il est pair. est alors pair 2k fois. Par suite, , le produit de par 2 est pair une fois de plus soit 2k+1 fois.

Or, on a écrit plus haut . Ceci implique que

Ce qui est tout simplement impossible car 2j est pair et 2k+1 est impair. La seule hypothèse faite ici est que pouvait s’écrire sous forme de fraction. Ce nombre ne peut donc pas s’écrire de cette manière sinon on aura des contradictions, il est “irrationnel”!
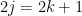
L’idée Pythagoricienne était alors détruite pour toujours, il existait des nombres non rationnels, que l’on ne pouvait pas écrire sous forme de fraction. rentre aussi dans cette catégorie de nombre, cela a été démontré en 1761 par Lambert. La démonstration est plus compliquée que pour donc non détaillée ici, mais les curieux pourront en trouver quelques éléments dans livre de Jean-Paul Delahaye cité en fin de dossier.

La preuve de l’irrationalité de réduit à néant aussi l’un des intérêts de recherches de décimales de (qui occupe encore aujourd’hui plusieurs personnes et supercalculateurs). En effet, un nombre rationnel a la propriété qu’à partir d’un certain nombre de décimales, on voit apparaitre un “cycle” :

1/3=0.333333333333… Le 3 est infiniment répété dès la première décimale
22/7=3.1428571428571428571… dès la première décimale, la suite de chiffres 142857 est répétée

Un des buts que pouvaient avoir le calcul des décimales de était de trouver ce cycle. La preuve de l’irrationalité de amena le fait qu’on ne trouvera jamais de cycle dans ses décimales.

Si et ont la propriété commune d’être irrationnels, il subsiste une très grande différence entre les deux : À partir d’un segment de longueur 1, je peux avec une règle non graduée et un compas tracer un segment qui fait exactement , la diagonale du carré. Qu’en est-il pour ?

Pi n’est pas aimé des carreurs

Autour de -500 (maintenant que les nombres relatifs sont définis, je peux les utiliser pour représenter les années), un grec nommé Anaxagore se posa un problème à la fois extrêmement élégant (tout le monde peut le comprendre et penser le résoudre facilement) et très dur à résoudre (plus de 2000 ans d’histoire ont été nécessaires pour trouver la réponse). Ce problème est celui de la “quadrature du cercle”. Le principe est de tracer un cercle et un carré faisant la même aire. Comme tout problème, il y a quelques règles à respecter :

• On ne doit utiliser qu’une règle non graduée et un compas
• Le nombre de tracés intermédiaires doit être fini (on ne peut pas en proposer une infinité)

L’impossibilité de quarrer le cercle (c’est le nom technique de la chose) a été démontrée en 1882. Mais l’apparente simplicité du problème a amené certaines personnes à continuer à essayer de trouver une construction pour quarrer le cercle, à tel point qu’une maladie existe pour les personnes qui veulent à tout prix résoudre la quadrature du cercle : “morbus cyclometricus”! Avant la démonstration de l’impossibilité, l’académie des science croulait sous les démonstrations (erronées bien entendu) du résultat à tel point qu’elle décida en 1775 qu’elle n’accepterait plus de regarder des démonstrations de la quadrature du cercle, elle avait probablement la conviction que c’était impossible.

Bien qu’assez élégant, énoncé comme cela il n’est pas simple de s’y attaquer rigoureusement. C’est cette imprécision qui a poussé plusieurs personnes à penser qu’elles l’avaient résolu. Construire un point à la règle et au compas veut dire que l’on a fait un nombre fini de constructions intermédiaires du type :

• Tracer une droite entre des points déjà construits
• Tracer un cercle dont le centre est un point déjà construit et le rayon est la distance entre deux points déjà construits.

Pour résoudre ce problème, il fallut faire le lien entre les constructions géométriques et les équations. Plusieurs mathématiciens renommés s’y sont attelés, de Descartes qui montra un lien entre certains type d’équations et les constructions à la règle et au compas jusqu’à Wantzel qui obtint l’équivalence entre les constructions géométriques à la règle et au compas et les “radicaux”.

Un nombre que l’on peut construire par radicaux est un nombre que l’on peut construire en un nombre fini d’étapes grâce aux nombres entiers et aux opérations racine carrée, division, multiplication, addition et soustraction. Ainsi,

est constructible par radicaux (à partir de 2 et de l’opération racine carrée)
est constructible par radicaux.

Grâce à cette formulation, le problème de la quadrature du cercle devenait : est-il constructible par radicaux? Wantzel démontra que non en 1837.

Les habitués des mathématiques réagiront vite en se demandant pourquoi se limiter aux racines carrées et ils auront bien raison! La notion de construction par radicaux a une grande valeur historique, mais aujourd’hui on parle davantage de nombre “algébrique”. Un nombre algébrique est un nombre qui est la solution d’une équation “polynomiale” à coefficients entiers. C’est-à-dire la solution x d’une équation du type :

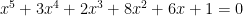
ou encore

En clair une équation avec des puissances de x, des coefficients entiers et s’annulant. Chose très rare en mathématique, les nombres qui ne sont pas algébriques portent un non moins évident que “non algébriques”, ils sont “transcendants”. Autre chose étonnante et pour le coup très liée à la démarche du mathématicien, la notion de nombre transcendant a été définie avant même que l’on sache s’il en existait. Heureusement, Liouville trouva des nombres transcendants et bien plus tard, en 1882, Lindemann démontra que était transcendant. Autrement dit, jamais aucune équation polynomiale à coefficients entiers n’aura pour solution !

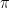
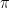
Pour résumer, n’est pas un entier, il ne peut pas être dessiné avec un compas et une règle, il n’est solution d’aucune équation algébrique, ce nombre est-il donc le plus compliqué qu’on puisse trouver, est-il rare de rencontrer des nombres de ce type?

Pourtant pi n’est pas bien compliqué

Comme nous venons de le voir, tout au long de l’histoire il a été démontré que le nombre était différent de la plupart des nombres que les mathématiciens rencontraient, c’est un nombre “transcendant”. Dans mon précédent dossier sur l’infini, nous avons vu qu’il existait plusieurs infinis plus ou moins grands. En particulier, j’ai présenté deux types d’infini, le dénombrable (celui que l’on peut numéroter) et l’indénombrable. Cantor a aussi démontré un résultat sur les nombres transcendants, ils forment un ensemble infini indénombrable alors que les nombres algébriques forment un infini dénombrable. Autrement dit, si l’on prend un nombre réel au hasard (si tant est que cela veuille dire quelque chose), il y a une probabilité nulle de tomber sur un nombre algébrique (comme 2 ou 3 ou , etc.). Autrement dit, ce n’est pas qui est rare, c’est plutôt tous les nombres que nous utilisons régulièrement!

En fait, appartient à un ensemble de nombres lui aussi dénombrable, celui des nombres “calculables”. Pour faire simple, un nombre calculable est un nombre duquel on peut approcher à une précision souhaitée en un nombre fini d’opérations. C’est à dire c’est un nombre dont le calcul jusqu’à n’importe quelle décimale peut être obtenu par un ordinateur. Tout comme la bibliothèque de Babel dans mon précédent dossier, l’ensemble de tous les programmes informatiques, de toutes les fonctions calculables est un ensemble dénombrable. L’ensemble des nombres que l’on peut calculer est donc infiniment plus petit que celui des nombres que l’on ne peut pas calculer. Autrement dit, en prenant un nombre réel au hasard, on a une probabilité nulle de tomber sur un nombre calculable… Les nombres Omega de Chaitin, dont je vous parlais en introduction sont justement des nombres incalculables. Il en existe même certains qui respectent beaucoup de très bonnes propriétés, mais dont on ne peut connaître aucune décimale!

Pour être complet sur les propriétés de pi, je me dois de préciser que le travail est loin d’être fini. Plusieurs résultats non démontrés subsistent : pi est-il un nombre univers (nombre dont tous les nombres entiers apparaissent dans les décimales)? Est-il un nombre normal (nombre dont les décimales suivent une certaine forme de hasard)?…

Puisqu’on a la chance d’avoir un nombre calculable, calculons-le!

La chasse aux décimales

Le calcul de décimales de n’a jamais cessé, depuis sa découverte, d’intéresser certains scientifiques. Pourtant cela ne sert pas à grand-chose… Depuis que l’on sait que est irrationnel, on sait qu’on ne trouvera pas de cycle dans ses décimales. Connaître plusieurs milliards de décimales n’aidera pas à savoir si oui ou non est un nombre univers ou un nombre normal. Mais pire encore, avoir plus d’une cinquantaine de décimales apporte beaucoup trop de précision par rapport à tous les calculs que nous serions amenés à faire. Par exemple, la seule connaissance de 40 décimales de suffit à calculer la circonférence de l’univers entier à la précision d’un atome d’hydrogène. Un des seuls intérêts mathématiques qui persiste serait de parvenir à trouver une régularité dans ces décimales, mais après plusieurs milliers de milliards de décimales connues, aucune n’est apparue.

En revanche, le calcul des décimales de pi a énormément fait avancer l’efficacité des méthodes calcul. Au début, les méthodes de calcul de reposaient sur la méthode des polygones présentée en début de dossier. Cette méthode permet de gagner trois décimales toutes les cinq étapes. Une autre méthode populaire est la méthode dite d' »arctangeante », c’est celle correspondant à la somme infinie présentée plus haut. Elle est tout aussi peu efficace que la méthode d’Archimède. C’est pourtant avec ces méthodes qu’est dépassée la centaine de décimales connues au XVIIIe siècle.

Au XIXe siècle, les calculateurs de décimales s’organisent. La 200e décimale est dépassée en 1844 par Von Strassnitzki, ou plutôt Johann Martin Zacharias Dahse, calculateur prodigue qui effectua la plupart des calculs! Le record continue à être battu par Shanks qui en 1874 calcule 707 décimales. Ce record est pratiquement le dernier record humain (il fut battu en 1945) et a une importance historique. D’abord parce que Shanks a passé 20 ans de sa vie à l’obtenir. Pour que ce type de calcul soit validé, il faut que quelqu’un le vérifie. Évaluons les deux possibilités pour la personne effectuant la vérification :

• Il trouve les mêmes décimales, Shanks deviens célèbre. Le vérificateur tombe dans l’oubli
• Il ne trouve pas les mêmes décimales. Cela ne prouve rien, il faut un autre vérificateur pour savoir qui a raison.

Autant dire que pour 20 ans de calcul, le jeu ne vaut pas tellement la chandelle. C’est une des raisons pour lesquelles le record résista d’abord jusqu’en 1945 et surtout jusqu’à l’apparition des premiers calculs par machine.

A la création du Palais de la Découverte à Paris en 1937, à l’occasion de l’exposition universelle, Borel décida de construire une salle dédiée à Pi. Ce lieu, unique salle au monde dédiée à pi (selon plusieurs sources mêmes si j’ai du mal à y croire), a été construite sur une base circulaire et avec un plafond formant une demi-sphère. Tout autour, les décimales de Shanks y ont été affichées. En 1945 avec le nouveau record et avec les records suivants, on eut la certitude que le calcul de Shanks était faux à partir de la 528e décimale. Les décimales du Palais de la Découverte ont donc été fausses jusqu’en 1945, mais contrairement à beaucoup de rumeurs, elles ont été corrigées depuis. Vous pouvez vérifier vous même en cherchant au-dessus du nom « Poisson » de la frise des mathématiciens les décimales « …0213949463… » on y lisait avant « …021395016… ». Ci-dessous une photo des décimales de la salle pi, mais n’hésitez pas à la visiter, elle existe encore!

L’ère des machines

Contrairement à ce que l’on pourrait croire, l’efficacité du calcul de pi par les ordinateurs ne dépend pas seulement de la puissance des ordinateurs, mais bien aussi du raisonnement mathématique utilisé. Il est même amusant de remarquer qu’historiquement les scientifiques se sont beaucoup plus intéressés à la façon de moins faire de calculs depuis que ce n’est plus eux qui les font. Par exemple, pour calculer

on effectue trois opérations (une addition et deux multiplication). Alors que si l’on factorise le calcul,

on effectue plus que deux opérations! Soit un gain de temps de 30%!

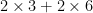
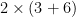
Ce sont donc des raisonnements mathématiques à la fois sur la complexité (nombre d’opérations à effectuer) et sur les propriétés de qui ont permis à travers les années de battre les records sur pi. En 1973, le million de décimales est dépassé par Guilloud et Bouyer qui utilisent la même formule que Shanks. La vérification de ce calcul a été effectuée par le CERN, à Genève et le résultat a été publié (oui oui, il s’agit bien d’un ouvrage ne contenant pratiquement que des décimales de pi!).

Aujourd’hui, le milliard de décimales est largement dépassé. En décembre 2009, le français Fabrice Bellard établit le record vérifié de 2700 milliards de décimales calculées avec un simple ordinateur de bureau. En octobre 2011, les Japonais Yee et Kondo affirment avoir calculé 10 000 milliards de décimales, résultat pas encore totalement validé à ma connaissance. Depuis que l’on connaît autant de décimales, il a été vérifié que toutes les dates de naissance (groupes de 6 chiffres) apparaissent, vous pouvez même chercher la vôtre ici.

Pour finir, Pi est donc un nombre qui de tout temps a passionné les scientifiques. Les propriétés et anecdotes rapportées ici ne sont qu’une infime partie de son histoire. Si le sujet vous intéresse, n’hésitez pas à consulter les livres ci-dessous.

Sources :
– Le fascinant nombre Pi de Jean-Paul Delahaye. Le livre à lire si le sujet vous intéresse, il est complet et simple d’accès, un must!
– Alex au pays des chiffres de Alex Bellos. Un livre très général et très agréable à lire, il contient un passage sur pi intéressant.
– La fabuleux destin de V2 de Benoit Rittaud. J’y ai trouvé la démonstration de non rationalité de racine de 2. C’est un excellent livre sur ce nombre.
– Calculer pi avec la pluie (merci Mathieu): http://amazings.es/2012/02/29/calculando-pi-con-gotas-de-lluvia/
– Des anecdotes sur le jour de pi ici : http://www.piday.org/stuff/
– Un WWsh qui parle de PI, queqlues exemples de WTF sonores autour de pi : http://www.linaudible.com/2011/03/19/wwsh065/

Cet article est une reproduction du dossier que j’ai écrit pour Podcastscience et je vous engage à vous abonner à ce podcast. Pour les plus flemmards, le texte et l’audio...